MATLAB 实习教程：经典算法与图形绘制

"MATLAB生产实习课程设计2，主要涉及经典算法的应用，通过MATLAB实现各种函数图形的绘制、极限分析、导数计算、多元函数微分、积分计算以及代数综合问题的解决。课程旨在深化对函数性质的理解，掌握MATLAB进行数值计算和图形描绘的技能。" 在本次实习中，学生将学习并实践以下知识点： 1. 函数图形画法：通过MATLAB的`plot`函数绘制不同类型的函数图形，如正切函数`tan(x)`、反正切函数`arctan(x)`、双曲正弦函数`sinh(x)`等。同时，了解如何画出水平渐近线，以及使用不同的线型区分不同的函数。 2. 极限与连续：利用函数图形理解函数的极限，例如观察正切函数和反正切函数在特定点的极限行为，以及通过图形判断函数的连续性。 3. 导数及应用：实习可能涵盖导数的计算，如通过MATLAB的符号计算功能`syms`和`diff`求解函数的导数，并理解导数在确定函数增减性、拐点等方面的作用。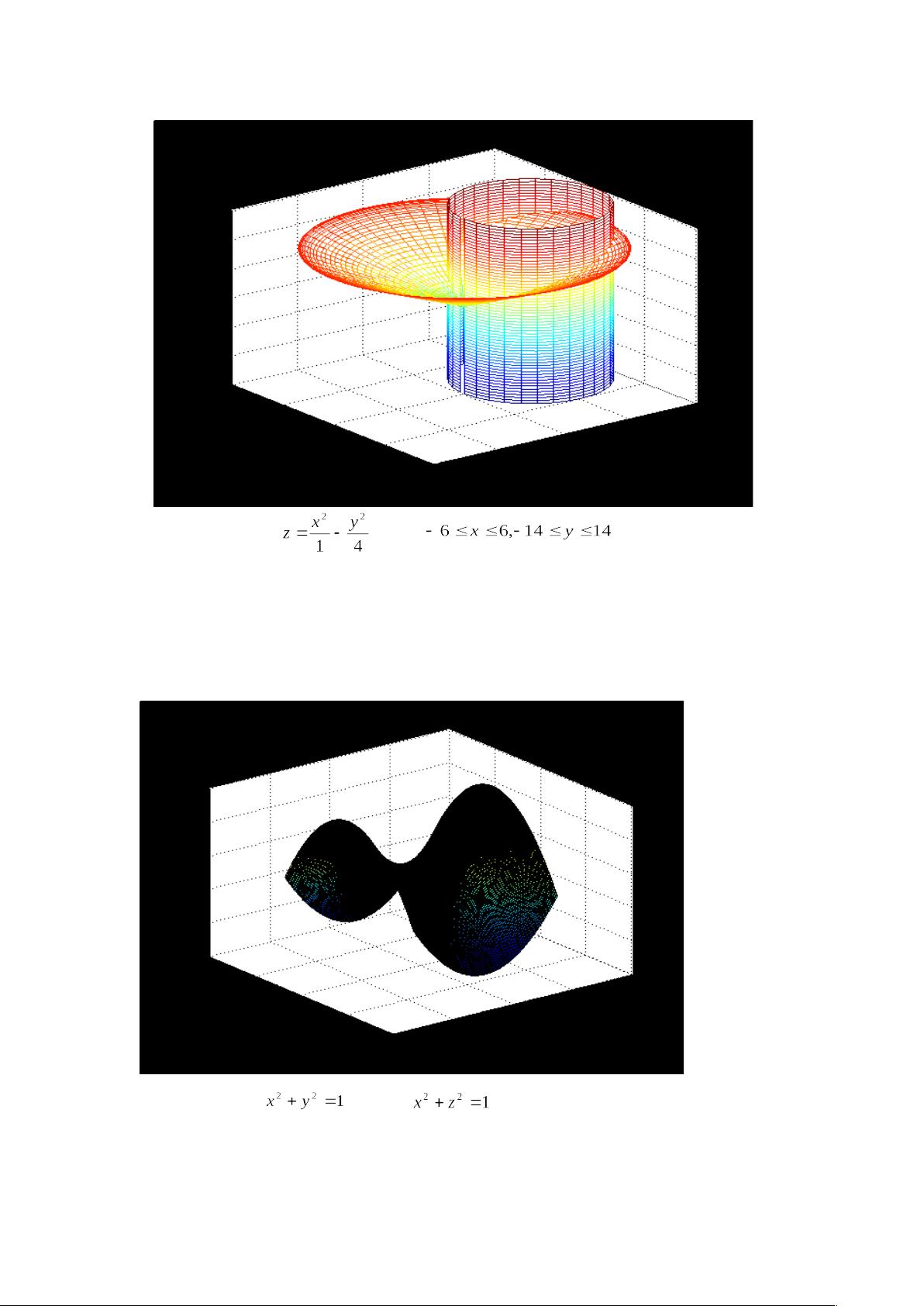 4. 多元函数微分学：可能涉及到多元函数的偏导数和梯度矢量，使用MATLAB的`grad`函数进行计算，并绘制等高线图或三维表面图来直观展示多元函数的几何特性。 5. 一元函数积分学：学习如何使用MATLAB的`integral`函数进行定积分和不定积分的计算，理解积分在面积计算、物理问题解决中的应用。 6. 代数综合：解决包含分段函数的代数问题，例如通过循环结构和条件语句`if`构建分段函数的图形，理解分段函数的性质。 7. 隐函数曲线：运用MATLAB的`ezplot`函数绘制由隐含方程定义的曲线，例如椭圆和双曲线，这有助于理解曲线的几何特征和解析解的关系。 8. 极坐标系统：使用MATLAB的`polar`函数画出极坐标下的图形，如对数螺线和五叶玫瑰线，熟悉极坐标系统下曲线的表示方法。 通过这些实习任务，学生不仅可以掌握MATLAB的使用，还能深入理解数学概念，提高问题解决能力，为未来在工程、科研等领域的工作打下坚实基础。