数字电路考题解析：逻辑代数与编码难题

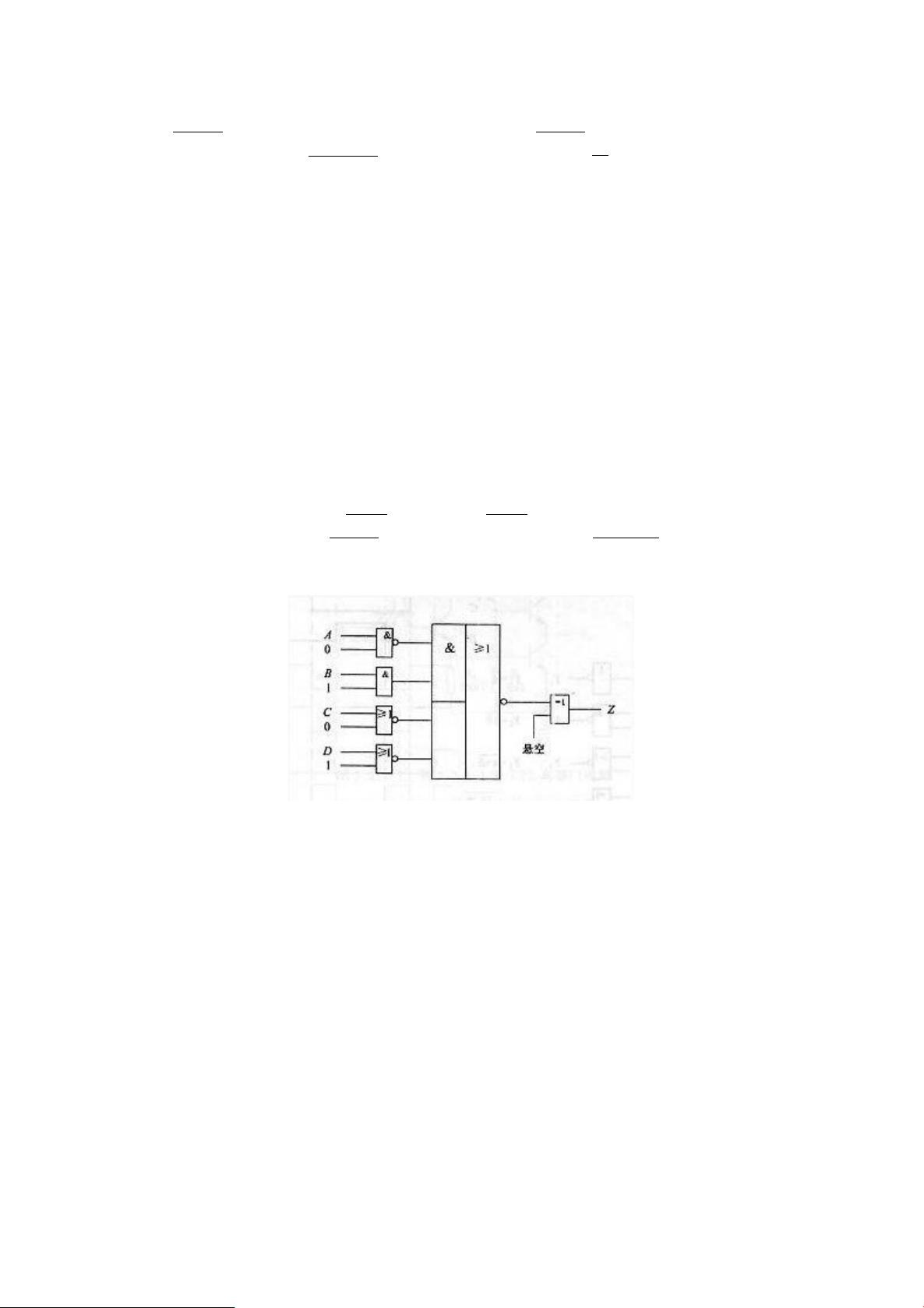
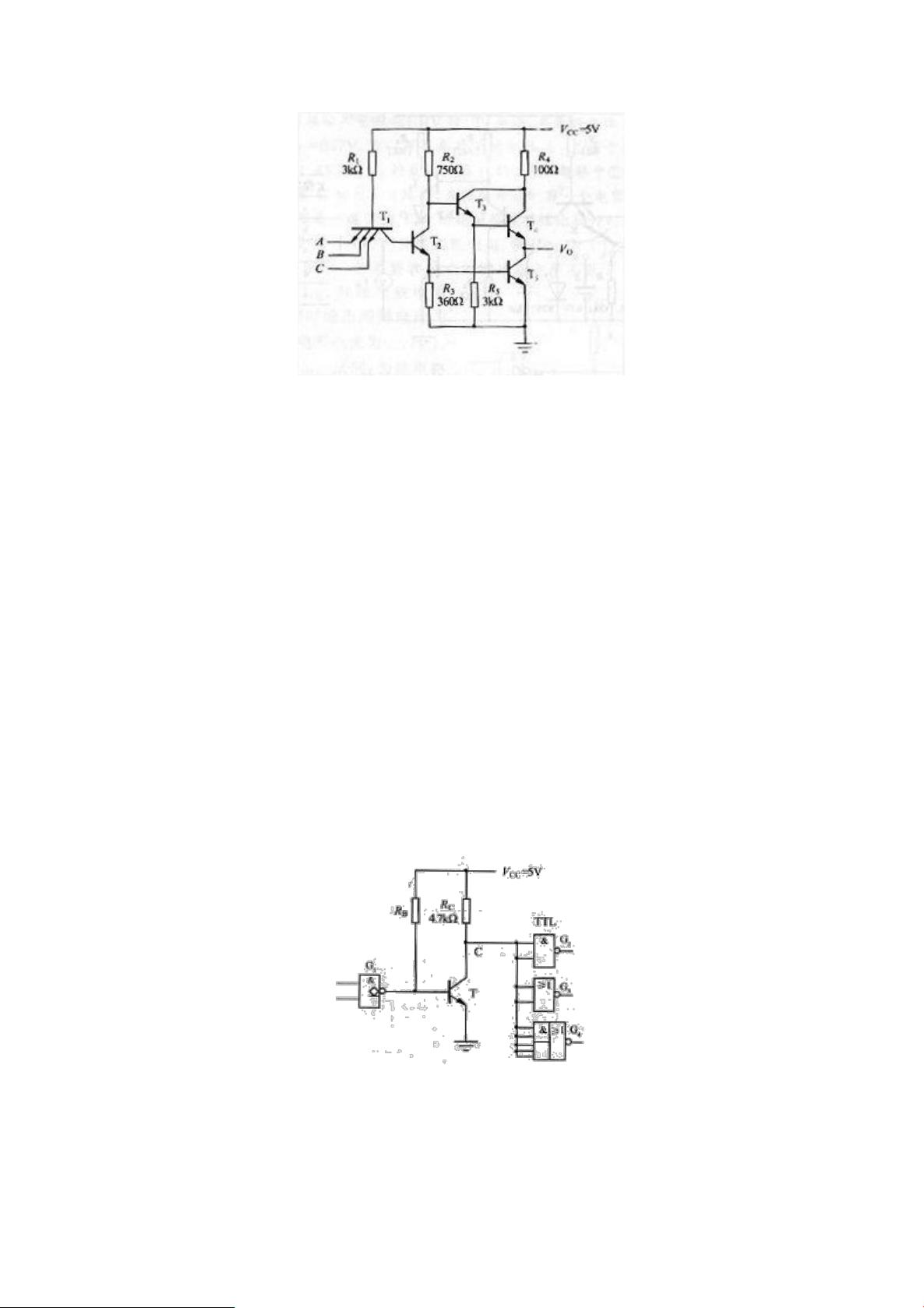
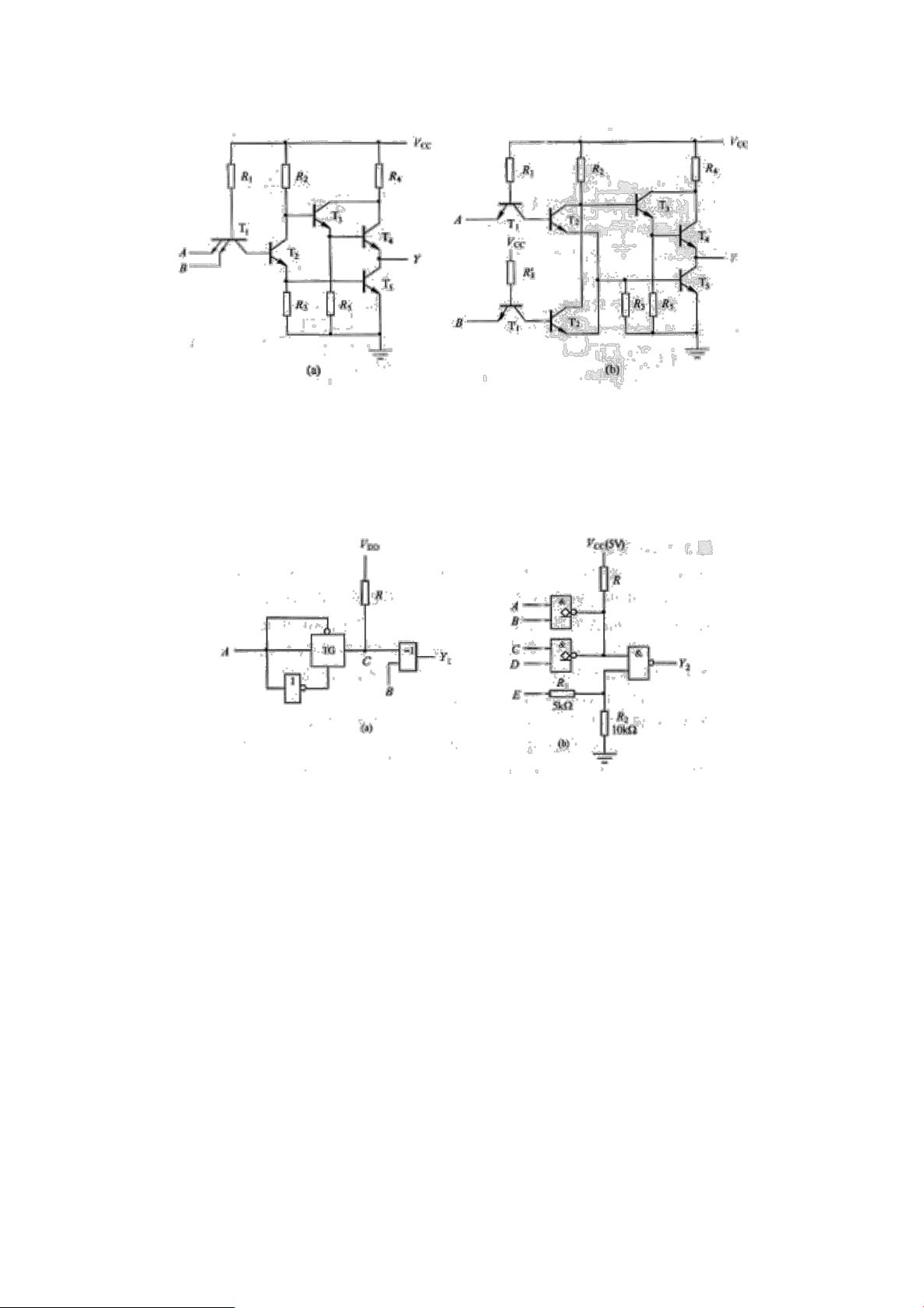
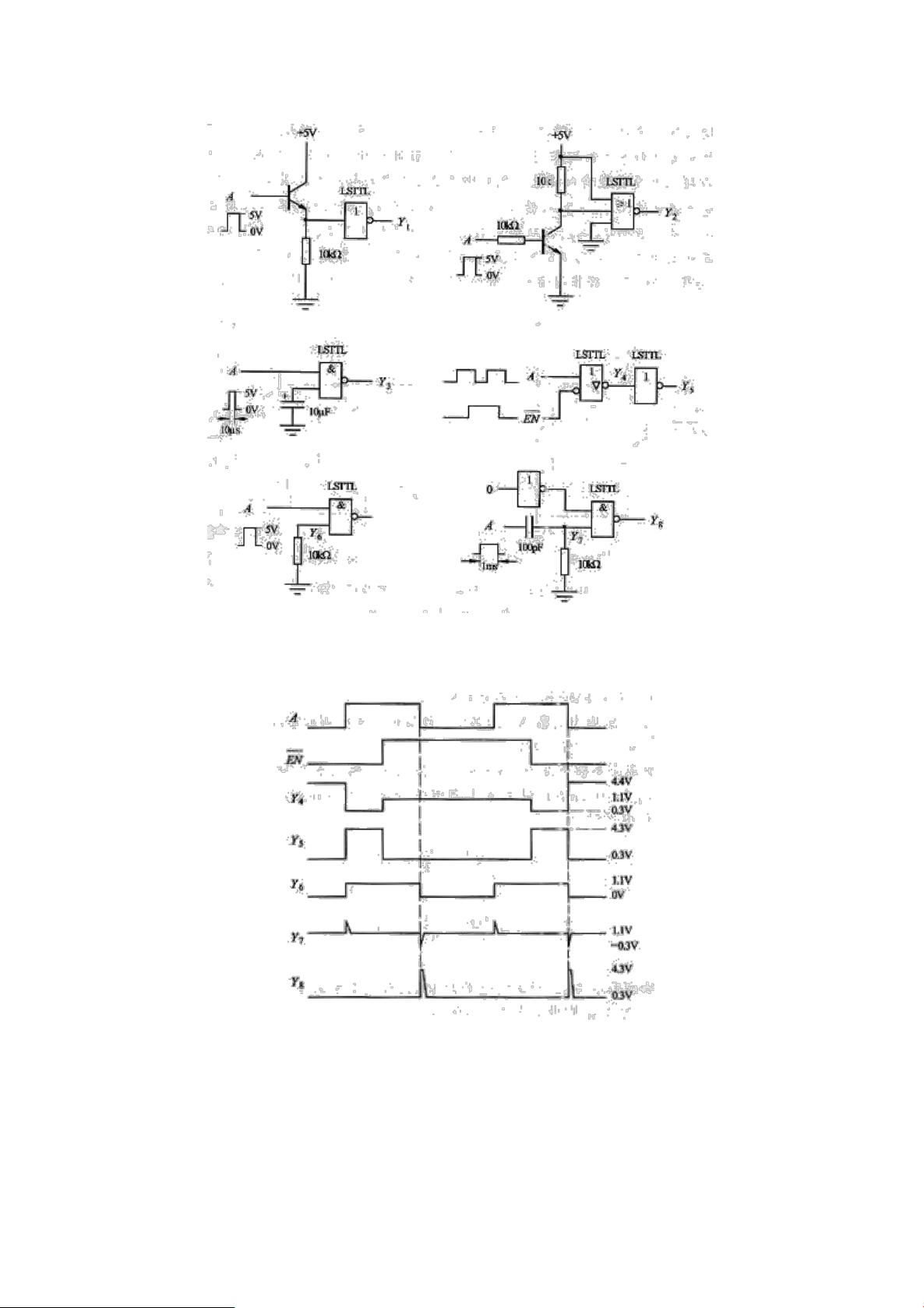
"此资源是关于数字电路的复习资料，包含了多所重点高校历年来的考题及详尽解答，主要涵盖数制与编码、逻辑代数等基础知识。" 在数字电路的学习中，数制与编码是基础中的基础。例如，一个8位二进制数A能否被8（10）整除，可以通过检查其最后三位是否全为0来确定，因为8的二进制表示是1000，只有当A2、A1、A0均为0时，二进制数A除以8的余数才为0。而题目中给出的解答过程正是基于这个原理。此外，了解不同进制之间的转换和比较也是必要的，如题目中提到的376.125D、576.1Q、110000000B、17A.2H这四个数的大小排列，需要将它们转换到同一进制进行比较。 逻辑代数是数字电路的核心内容，它包括基本的逻辑运算和逻辑函数的化简。例如，题目中列举了判断逻辑关系正确与否的问题，如"若A=B，则AB=A"是正确的，因为A与B相同，它们的乘积不变；而"若AB=AC，则B=C"是错误的，因为当A=0时，B和C可以取任意值。此外，逻辑函数的反演式和化简也是常考知识点，如L的反函数的求解，以及通过公式化简法或卡诺图法简化逻辑函数，例如F=(AB+C)(B+C)简化为C+BC，或者带有约束条件的逻辑函数F=D+C+BD+B'A的化简，这些都需要对德摩根定律、分配律、结合律等逻辑定律有深入理解。 在实际考试中，这些问题可能以填空题、判断题、计算题等形式出现，要求考生不仅掌握理论，还要具备快速准确计算的能力。因此，熟练掌握数制转换、逻辑运算规则、化简方法是备考的关键。通过这些考题和解答，学生可以检验自己的学习效果，找出知识盲点，从而有针对性地进行复习和提高。