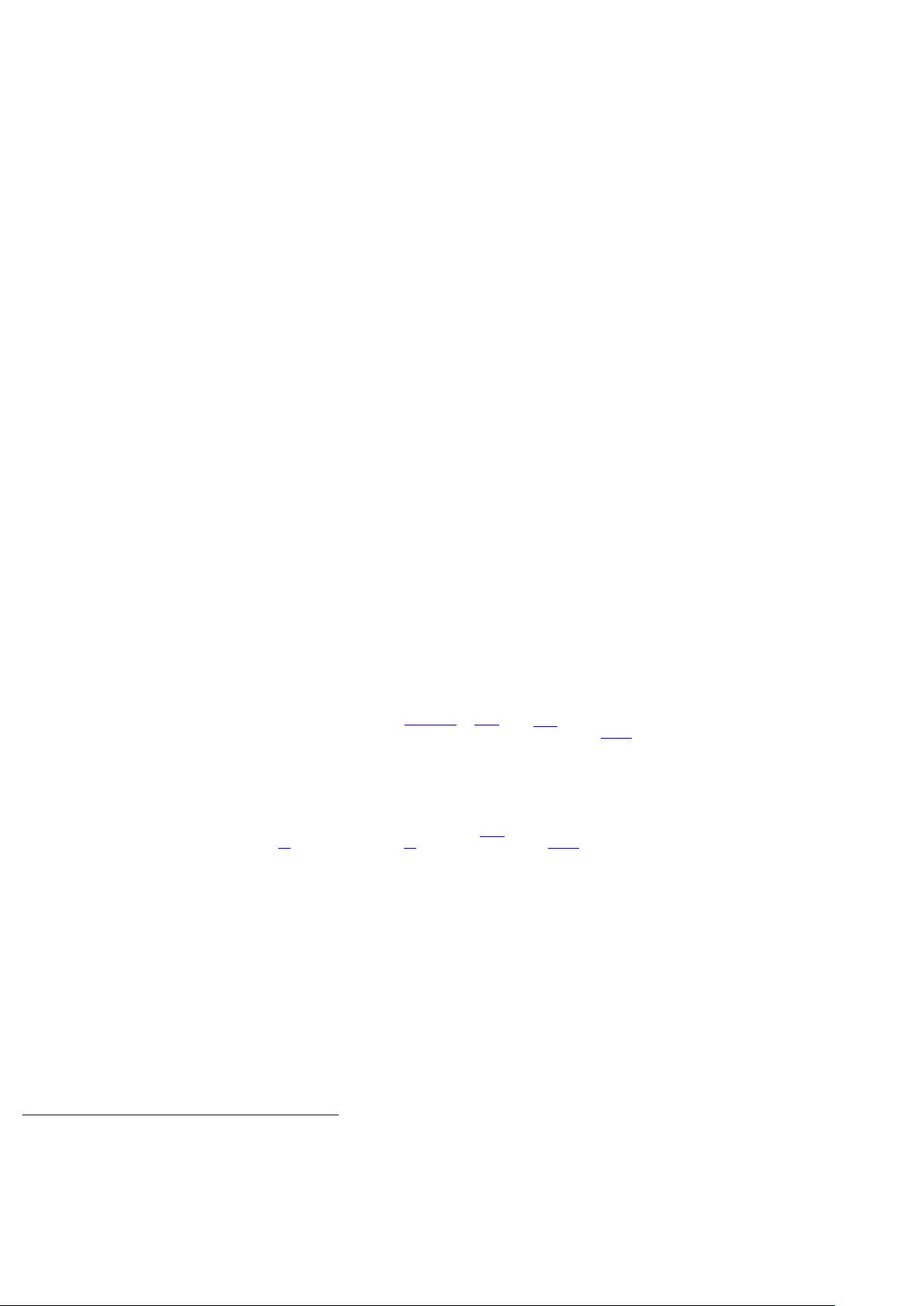MATLAB PDETOOL详解：轻松解决偏微分方程

"MATLAB的PDE工具箱是一个用于解决二维偏微分方程(PDE)的集成环境，提供了一个直观的图形用户界面，使得用户无需深入理解解题过程或编程即可解决问题。" 在MATLAB中，PDETOOL是解决偏微分方程问题的关键工具。通过输入`pdetool`命令，用户可以启动这个工具箱，它包含了多种问题类型的解法，适用于不同的科学和工程领域。PDETOOL将问题分为以下8种类型： 1. GenericScalar：适用于一般标量场的问题，比如简单的拉普拉斯方程。 2. Genericsystem：处理一般的偏微分方程组，适用于更复杂的情况。 3. StructualMechnics,PlaneStress和PlaneStrain：针对结构力学中的平面应力和应变问题。 4. Electrostatics：用于静电场的模拟计算。 5. Magnetostatics：处理静磁场问题。 6. AcPowerElectromagnetics：应用于交流电磁场的分析。 7. ConductiveMediaDC：解决直流导电介质问题。 8. HeatTransfer和Diffusion：涵盖了热传导和扩散问题。 PDETOOL的使用流程通常分为三个主要步骤： 1. 设置定解问题： - DrawMode：在这个模式下，用户可以绘制求解区域，支持各种几何形状的定义。 - BoundaryMode：定义边界条件，这是PDE问题的重要组成部分。 - PDEMode：指定方程类型和系数，可以根据问题的物理特性输入相应的PDE模型。 2. 解方程： - MeshMode：将定义的区域进行网格化，生成三角形网格，这对于数值求解是必要的。 - SolveMode：设置初始条件，并执行求解。对于本征值问题，还可以指定搜索的本征值范围。 3. 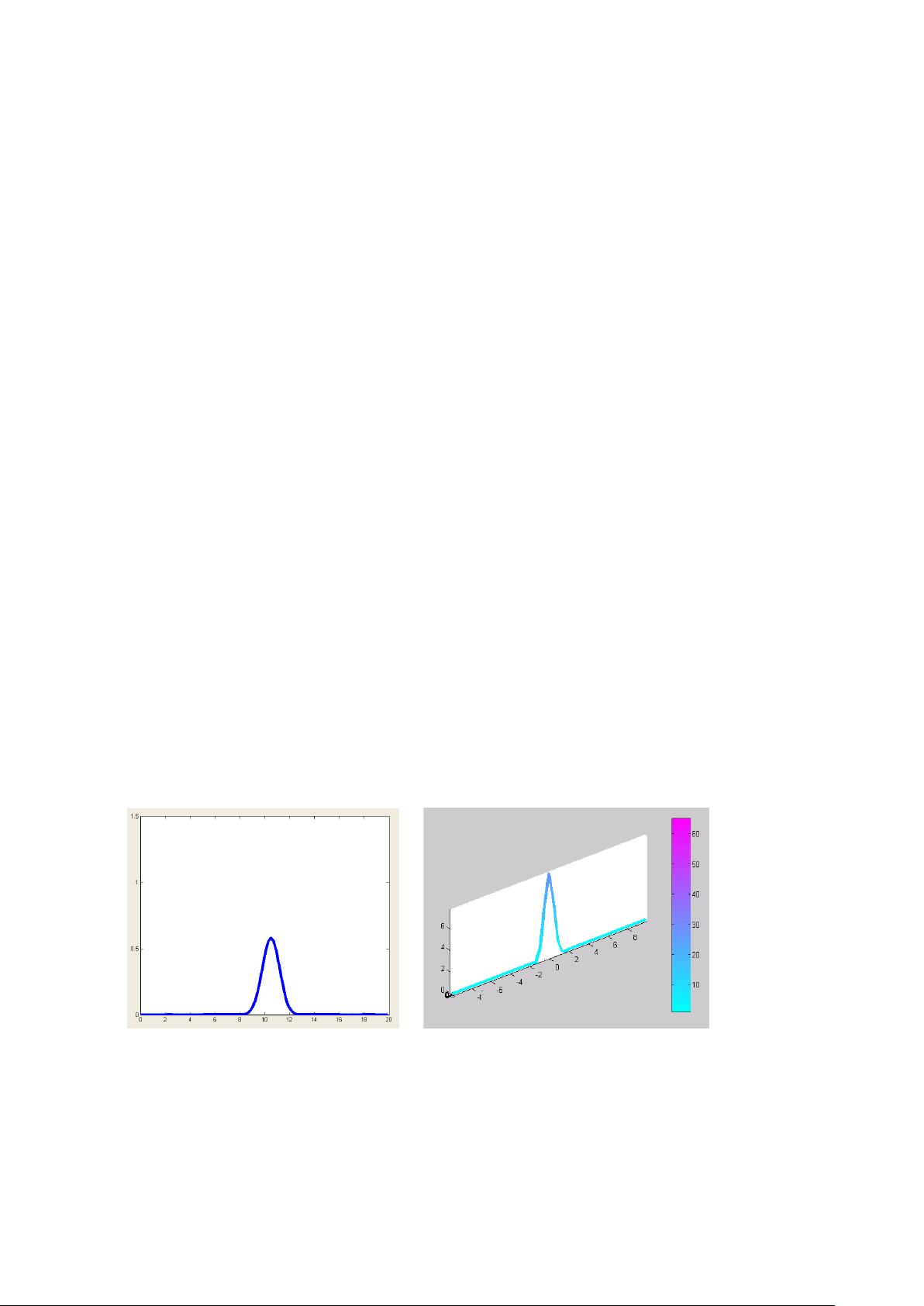结果可视化和输出： - PlotMode：提供多种图形表示方法，如彩色图、高度图、矢量场图、曲面图、网线图、等值线图和箭头图。对于时间依赖的方程，还能创建动画展示解随时间的变化。 例如，一个基础的用例可能是解决拉普拉斯方程或泊松方程，这在电学中常见，例如描述带电云与大地之间的均匀电场。用户可以通过PDETOOL设定问题的参数，比如电荷分布、电导率等，并观察解的分布和变化。 PDETOOL的这些功能使非专业编程者也能方便地处理复杂的偏微分方程问题，同时也为专业人士提供了一个快速验证理论和实验结果的平台。通过结合实际物理背景，用户可以在MATLAB环境中直观地理解和探索各种物理现象。