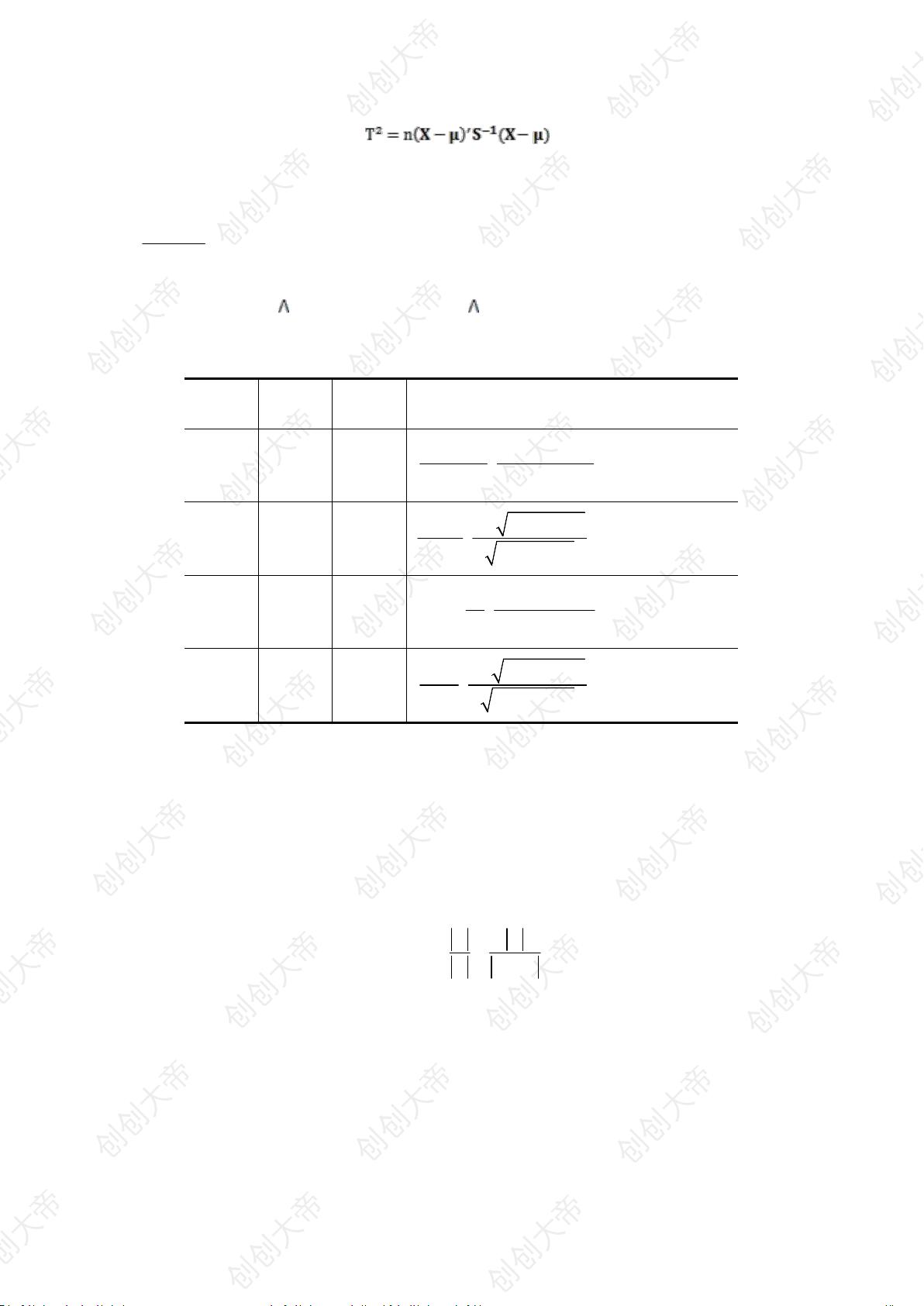
多元统计分析：矩阵方法与样本协方差矩阵

"该资源是朱建平教授编写的《应用多元统计分析》课程的课后习题答案，主要涉及多元统计分析中的概念和计算方法，包括数据的处理和统计量的估计。" 在多元统计分析中，我们经常会遇到如何估计总体协方差矩阵的问题。在给定的部分内容中，提供了两种不同的方法来估计总体协方差矩阵Σ。 方法1： 这是利用样本均值和样本数据计算样本协方差矩阵的方法。首先，我们计算样本均值，然后通过减去样本均值和求和来得到样本协方差。具体步骤如下： 1. 计算样本均值：\( \bar{X} = \frac{1}{n} \sum_{i=1}^{n} X_i \)。 2. 计算样本协方差矩阵：\( S = \frac{1}{n-1} \sum_{i=1}^{n} (X_i - \bar{X})(X_i - \bar{X})^\prime \)。 3. 最后，\( S \) 是Σ的无偏估计，因为除以的是 \( n-1 \) 而不是 \( n \)。 方法2： 这种方法也是基于样本数据，但使用了中心化变量 \( X_i - \mu \)，其中 \( \mu \) 是总体均值。步骤如下： 1. 首先，计算中心化变量：\( X_i - \mu \)。 2. 然后，计算中心化变量的乘积：\( (X_i - \mu)(X_i - \mu)^\prime \)。 3. 最后，再次通过求和和除以 \( n-1 \) 得到样本协方差矩阵 \( S \)。 在2.9题中，给出了一个多元正态分布的样本 \( X_1, X_2, ..., X_n \)，其来自 \( N_p(\mu, \Sigma) \)。这里的任务是找到样本协方差矩阵 \( S \) 的分布。当样本大小 \( n \) 足够大时，\( S \) 遵循Wishart分布，记为 \( W_p(n, \Sigma) \)。Wishart分布是多元正态分布样本协方差矩阵的自然对数似然函数的最大似然估计的分布，它在多元统计推断和假设检验中扮演着重要角色。 总结来说，这部分内容涉及了多元统计分析中的样本协方差矩阵的估计及其性质，对于理解和应用多元统计分析方法，尤其是涉及随机样本的统计推断时，这些概念和公式至关重要。在实际数据分析中，正确估计协方差矩阵能够帮助我们理解变量间的相关性，进行回归分析、主成分分析等高级统计方法。