p-最优性准则下的多群多目标投资组合优化算法

"这篇文章介绍了一种名为p-MSMOEA的多群多目标优化器，该优化器专门设计用于处理多目标投资组合优化问题。基于p-最优性准则，p-MSMOEA避免了传统方法中通过加权系数法将多目标问题转化为单目标问题的转化过程，而是直接寻找Pareto最优解。通过结合p-最优性准则和多群策略，该算法实现了协同演化，提高了优化的精度和计算的稳定性。通过与其他多种多目标进化算法的比较实验，p-MSMOEA在数学基准函数和投资组合实例上的表现证明了其在投资组合优化问题上的优越性。" 本文的核心知识点包括： 1. **多目标优化**：多目标优化（Multi-objective optimization，MOO）是解决具有多个相互冲突的目标函数的优化问题，投资组合管理就是这样的一个典型应用场景，需要在风险和回报之间寻找平衡。 2. **投资组合优化问题**（Portfolio Optimization Problem，POP）：这是金融领域的一个关键问题，涉及如何在不同的投资项目之间分配资金以最大化收益并控制风险。由于其复杂性，被归类为NP难题。 3. **进化算法与群体智能优化**：进化算法（Evolutionary Algorithms，EAs）和群体智能优化器常用于解决这类复杂优化问题，如粒子群优化、遗传算法等。在本文中，它们被用于处理多目标投资组合优化问题。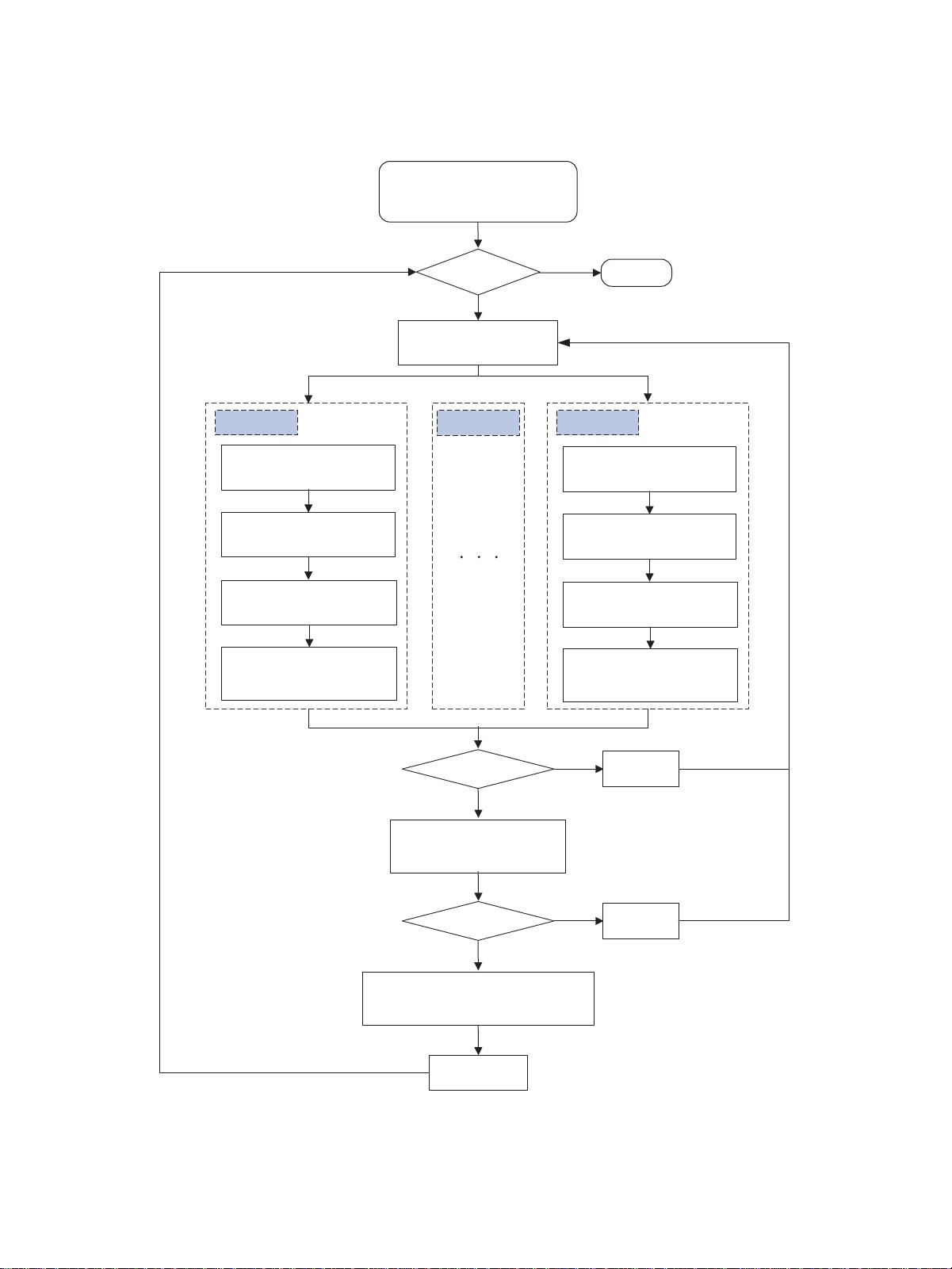 4. **p-最优性准则**：p-最优性准则是一种衡量多目标优化问题中解集质量的方法，它寻求找到所有Pareto最优解，而不仅仅是通过加权平均得到的单一解决方案。 5. **多群策略**（Multi-swarm strategy）：这是一种分布式优化策略，通过多个独立的群体（或“种群”）协作搜索解决方案空间，可以提高算法的探索能力和全局优化性能。 6. **协作协同进化**（Cooperative co-evolution）：p-MSMOEA采用了这种策略，使得各个群体能互相学习，共同提升整体优化效果。 7. **比较实验与评估**：为了验证p-MSMOEA的有效性，文章进行了大量的实验，包括在六个数学基准函数和两个实际投资组合案例上的对比测试。实验结果表明p-MSMOEA在优化精度和计算稳定性上优于传统的多目标进化算法。 这些知识点在金融投资、优化理论、机器学习以及算法设计等领域都有广泛的应用价值。p-MSMOEA的提出为多目标投资组合管理提供了新的解决思路，有助于更好地平衡风险和收益，实现更有效的资产配置。