控制系统数学模型：从微分方程到传递函数

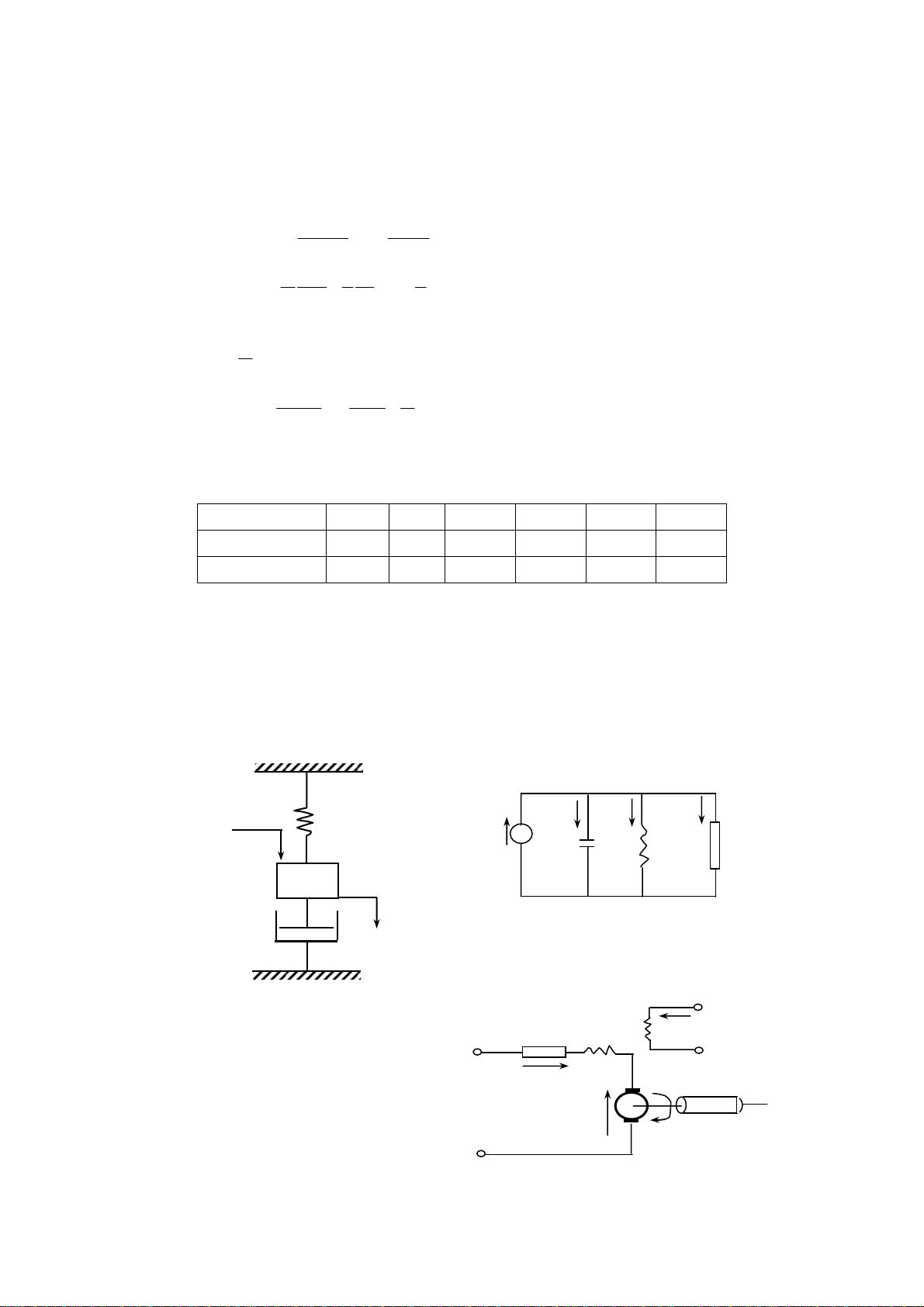
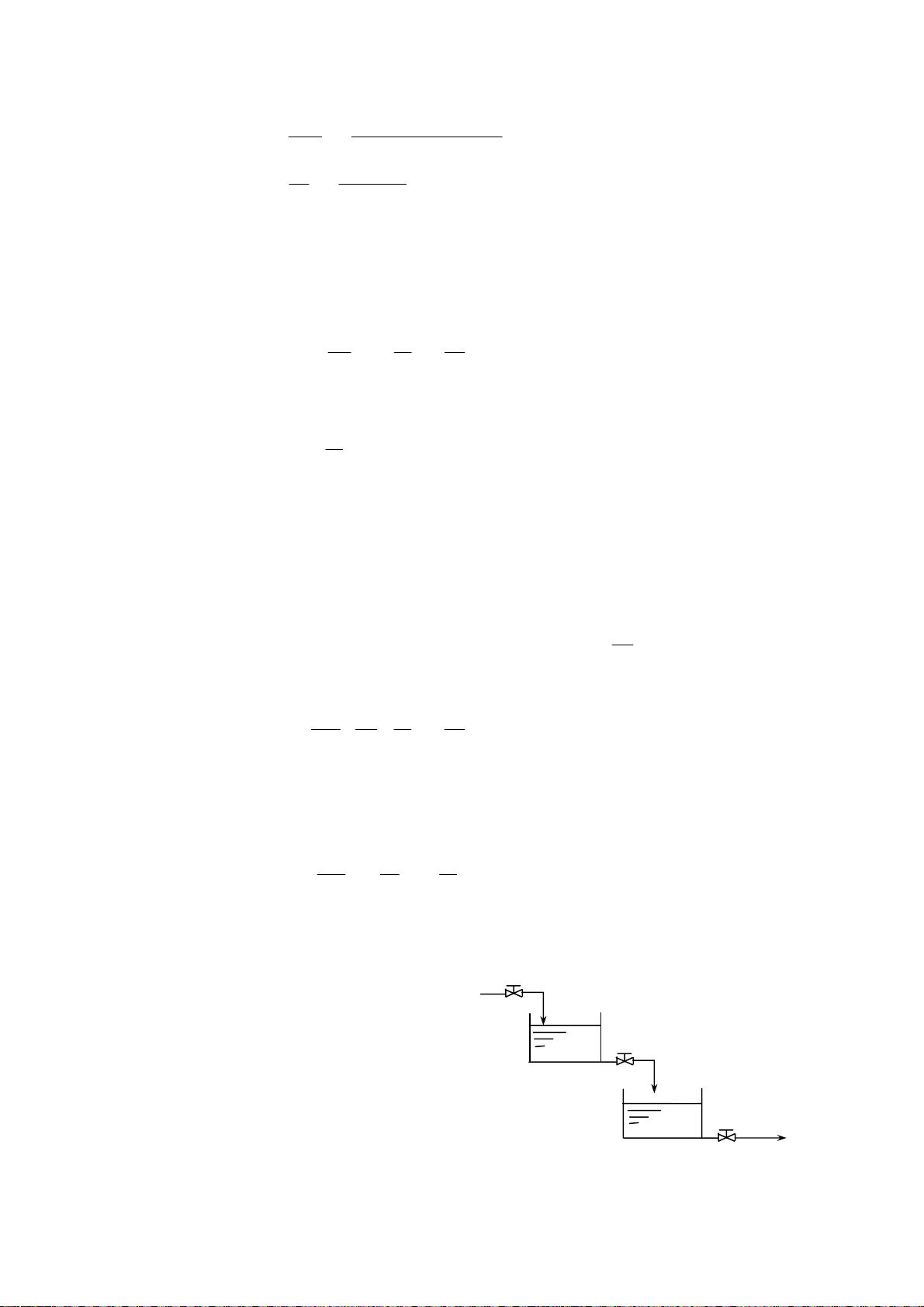
"该资源详细探讨了连续时间控制系统的数学模型和设计，涵盖了从微分方程模型到状态方程，再到传递函数、方块图、信号流图等多种建模方法，以及各种数学模型之间的转换关系。" 在控制系统设计中，连续性是一个至关重要的概念，因为它直接影响着系统的稳定性和性能。连续时间控制系统的数学模型是理解和设计此类系统的基础。本资料首先介绍了如何通过微分方程来描述系统的动态行为，列举了多个实际系统（如R-L-C电路、机械动力学系统、直接蒸汽加热器和汽车控制系统）作为建模的例子，并详细讲解了如何列写微分方程以及微分方程的特征。 接着，资料深入讨论了状态空间建模，包括状态变量的选择（物理量或相变量）以及状态方程的建立。状态空间模型能够更全面地描述系统的行为，有助于进行控制设计。此外，还涵盖了特殊特性的建模，如纯滞后、分布参数、积分、高阶特性以及非线性特性的线性化处理。 控制系统的其他关键组件，如控制器（PID和MAC）、测量元件（测速发电机和热电阻）以及执行机构的数学模型也得到了阐述。这些组件的模型对于理解整个系统的行为至关重要。 然后，资料讲解了传递函数和方块图，这是分析线性系统常用的方法。传递函数提供了系统的频率响应信息，而方块图则方便了系统分析和综合。同时，还介绍了信号流图和梅逊增益公式，这是一种用于计算系统增益和反馈路径的工具。 最后，资料讨论了不同数学模型之间的转换，包括如何从微分方程求解状态方程，从状态方程得到传递函数，以及通过状态变换保持系统特征值的不变性。这些转换能力使得工程师可以根据实际情况选择最适合的建模方法。 这份资料详尽地阐述了连续时间控制系统的数学建模和分析，为理解和设计复杂控制系统提供了坚实的理论基础。无论是初学者还是经验丰富的工程师，都能从中受益匪浅。