详解隐马尔可夫模型：结构、概率计算与应用

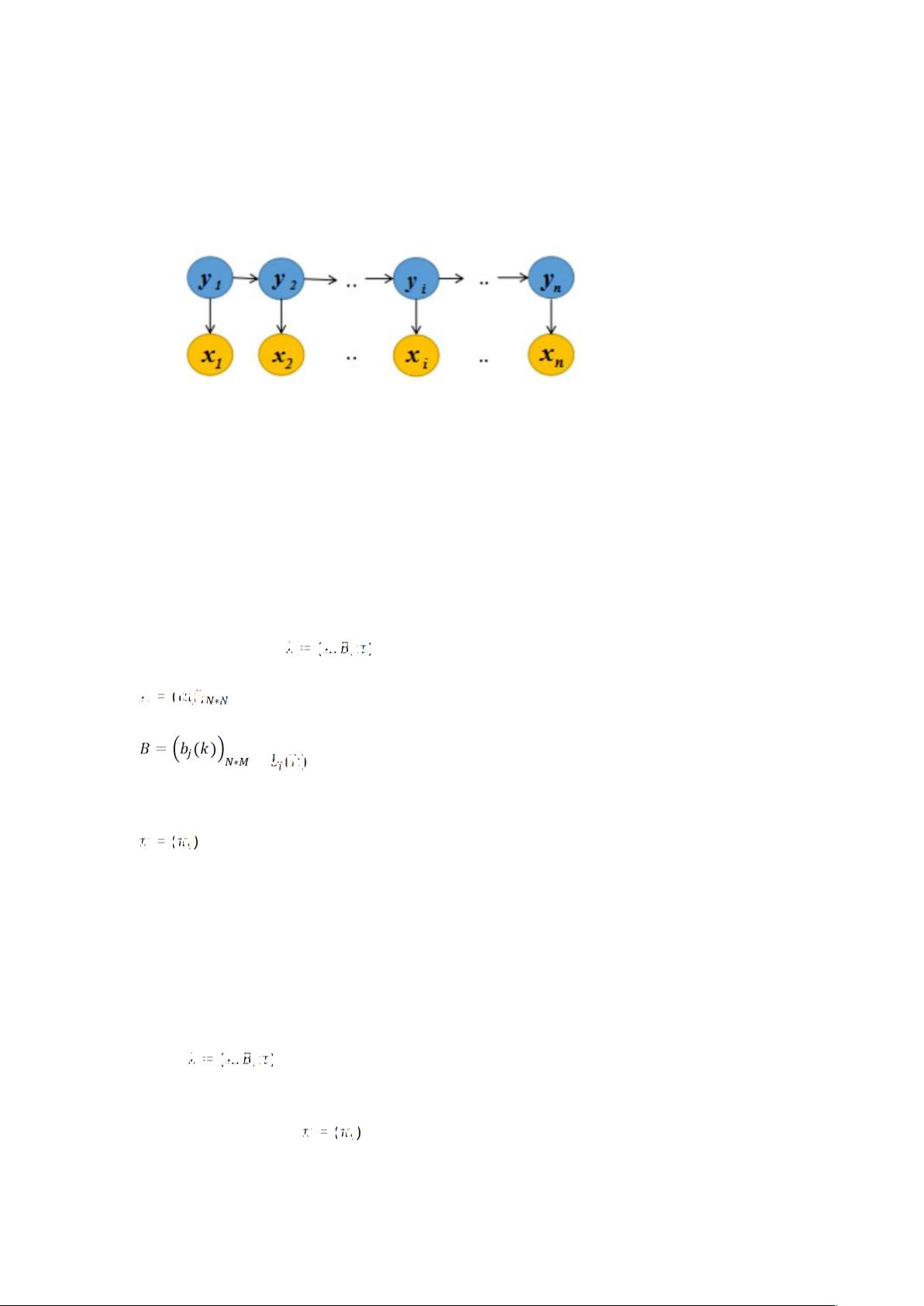
隐马尔可夫模型（HMM）是一种在统计学和计算机科学中广泛应用的模型，用于处理时序数据，特别是在语音识别、自然语言处理等领域。该模型主要由两部分组成：不可观测的状态序列和可观测的观测序列。状态序列{y1, y2, ..., yn}和观测序列{x1, x2, ..., xn}之间通过状态转移概率和观测概率联系。 模型的核心定义包括状态集Q={q1, q2, ..., qN}和观测集V={v1, v2, ..., vM}，分别表示可能的状态和观测值。状态转移概率矩阵aij给出了从状态qi到qj的概率，观测概率分布则定义了在特定状态下产生观测值vk的概率。初始状态概率向量定义了每个状态在时间t=1时出现的概率。 隐马尔可夫模型基于两个假设：齐次马尔可夫假设，即当前状态只依赖于前一个状态；观测独立性假设，认为观测值仅与当前状态相关。生成观测序列的过程涉及随机选择初始状态、按状态转移概率生成后续状态、并根据当前状态观测概率生成观测值。 在模型应用中，主要有三个关键问题： 1. 概率计算问题（评估问题）：求解给定模型和观测序列的情况下，观测序列发生的概率p(o|Q, A, B, π)。 2. 学习问题（参数估计）：已知观测序列，目标是找到最佳参数A, B, π，使观测序列的概率最大。 3. 预测问题（序列解码）：给定模型和观测序列，找到最可能的状态序列。 其中，前向算法是解决概率计算问题的重要方法，它计算出到每个时间点t的前向概率，即观测序列的累积概率。这个算法通过递推计算，避免了直接求解高阶乘积的复杂性，大大简化了计算过程。其他方法如维特比算法（Viterbi Algorithm）则用于解决预测问题，通过动态规划寻找最优状态路径。 隐马尔可夫模型是一种强大的工具，通过其概率模型和特定的计算方法，为序列数据建模提供了实用且高效的手段。在实际应用中，了解这些基础概念和算法对于理解和开发基于HMM的系统至关重要。