高阶系统简化：传递函数的Pade、Routh逼近与PID优化

"传递函数简化处理方法" 在控制系统设计和分析中，传递函数是一种常用且重要的数学工具，它能描述系统输入与输出之间的动态关系。高阶传递函数通常对应于复杂的系统行为，但随着系统复杂性的增加，直接处理高阶传递函数会变得极其困难，不仅计算量大，而且分析和控制设计的难度也会显著提升。因此，对高阶传递函数进行简化处理是必要的，以提高控制系统的精度并满足实际工程需求。 1. **传递函数简化方法** - **Pade逼近法**：Pade逼近法是一种利用有理函数近似高阶传递函数的方法，它通过对传递函数的级数展开，构造出与原函数在特定区间内具有良好匹配的Pade近似。这种方法的优点在于计算简便，且在低频段的逼近效果较好，适合用于设计PID控制器。 - **时间矩逼近法**：这种方法通过选取系统的时间响应特征值（如上升时间、峰值时间和超调量等）来构建低阶模型，以保持原系统的动态特性。 - **连分式逼近法**：连分式逼近法通过构造与原传递函数相似的连分式结构来近似高阶系统，其特点是设计过程相对直观，且在频域内的拟合精度较高。 - **Routh逼近法**：Routh阵列是稳定性分析的重要工具，Routh逼近法利用Routh-Hurwitz稳定性判据来构造低阶模型，保证简化后的系统具有与原系统相同的稳定性。 - **可调参数逼近法**：这种方法允许在保持系统主要动态特性的同时调整参数，以适应不同的工程需求。 2. **PID参数降阶设计** 在简化高阶系统后，通常会采用PID控制器进行控制设计。Pade降阶法可以将低频信息提取到PID参数中，使得设计过程更加直观且易于优化。 3. 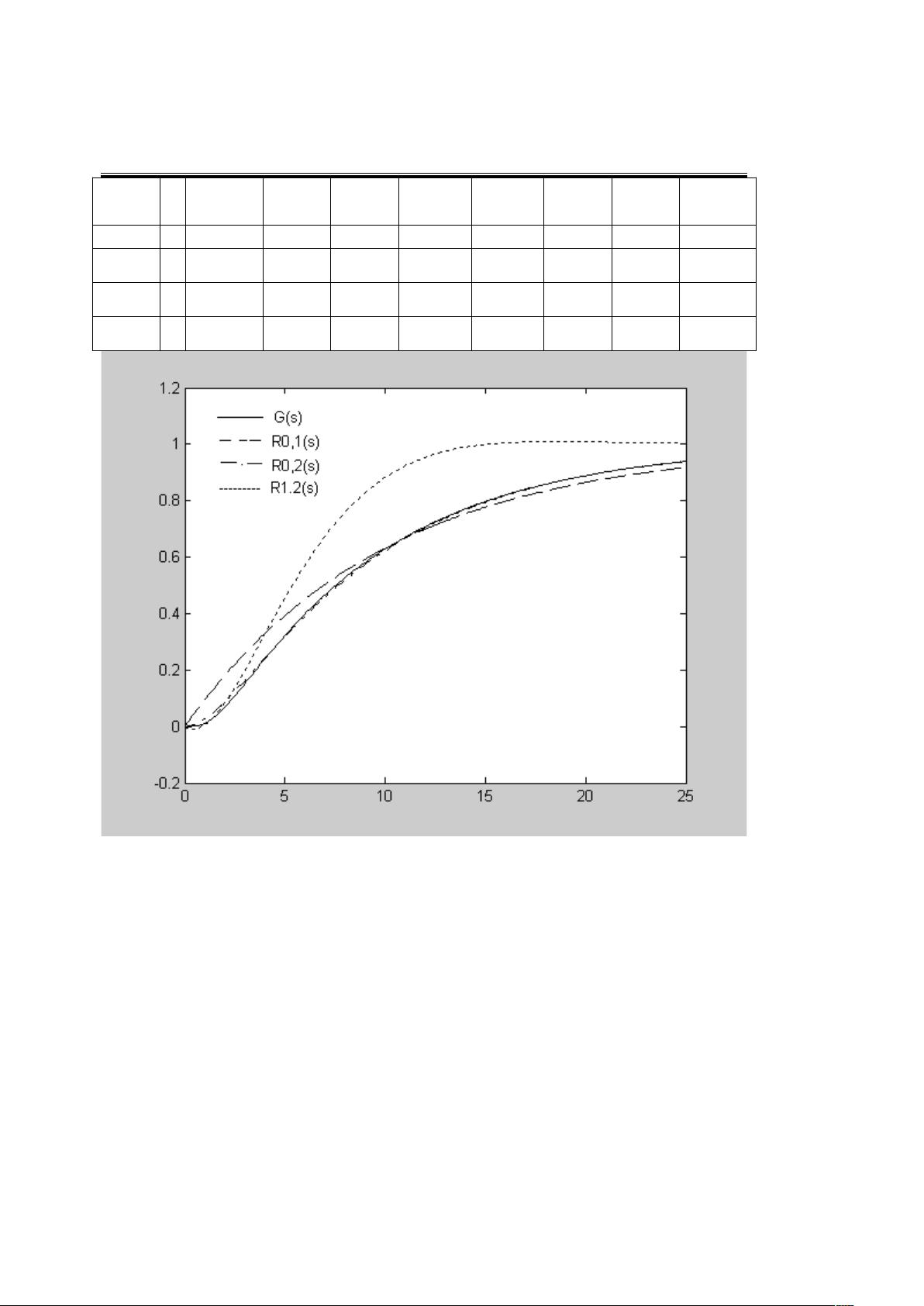**实例应用与比较** 文中通过四阶R-C梯形网络的方框图解耦例子，展示了简化方法在网络模拟和计算中的有效性。各种方法的优缺点和适用范围也在实例中得到体现，比如Pade逼近法适用于对低频响应要求较高的场合，而Routh逼近法则更注重系统的稳定性。 4. **连分式法研究** 连分式法在频域降阶方法中具有较为清晰的设计思路和较高的拟合精度，适用于需要精确匹配高阶系统动态特性的场景。 5. **总结** 传递函数简化处理方法是解决复杂系统控制问题的关键步骤，它能够有效地降低分析和设计的复杂性，提高控制系统的精度和实用性。在选择简化方法时，应根据系统的具体特性和工程需求来权衡各种方法的优缺点，以实现最佳的控制性能。