理解交叉熵损失函数：从信息论到深度学习

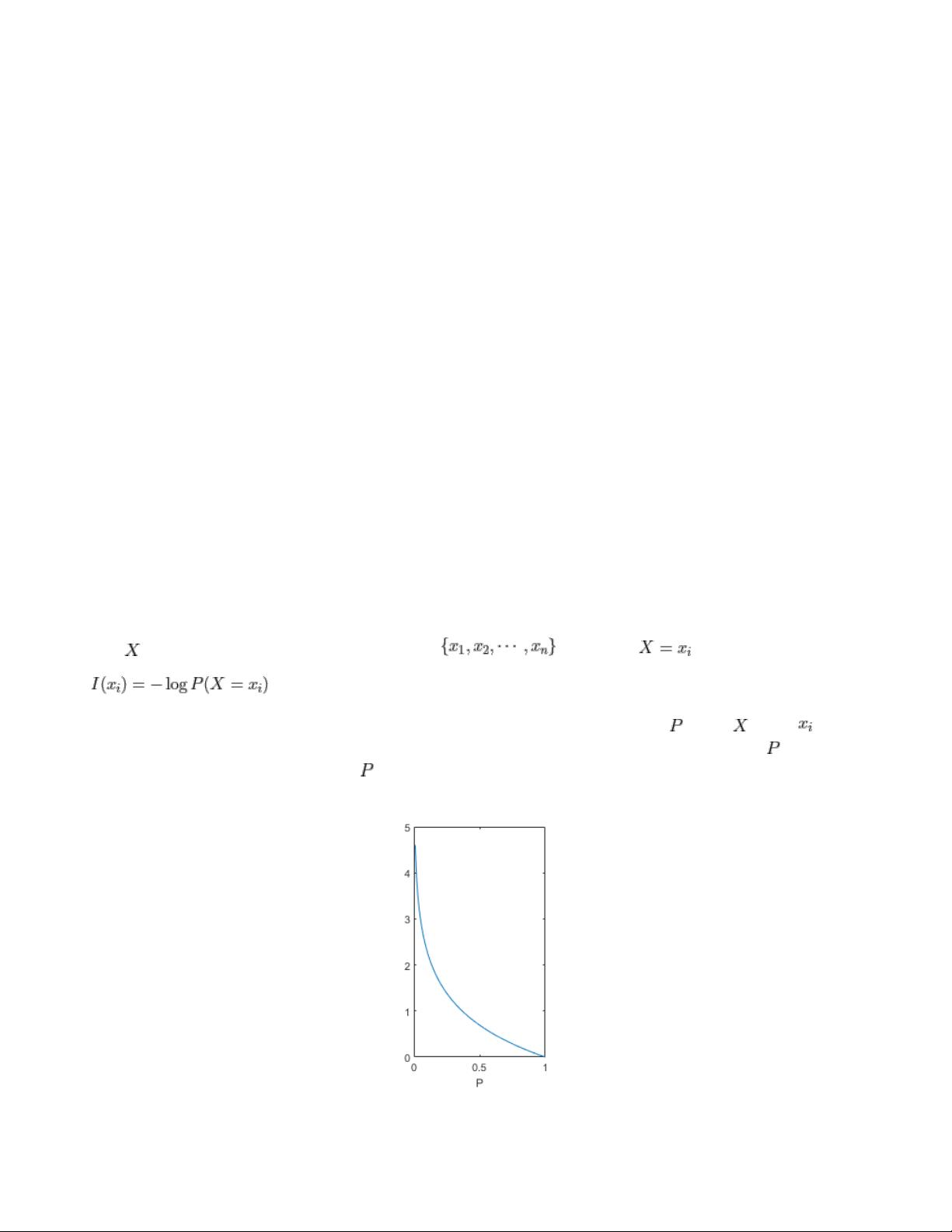
交叉熵损失函数（Cross Entropy Loss）是人工智能领域中常见的损失函数，尤其在分类任务中被广泛使用。它源自信息论的概念，包括信息量和熵的理论基础。 交叉熵（CrossEntropy）是衡量两个概率分布之间差异的度量。在机器学习中，通常将实际的（或理想的）概率分布与模型预测的概率分布进行比较。它反映了模型预测的准确度，特别是在多分类问题中，用于评估模型预测类别概率的准确性。 1. 信息量（Information）是描述事件发生信息含量的量。一个事件的信息量与其发生的概率成反比，即非常可能发生的事情信息量低，而罕见事件的信息量高。信息量的计算公式为：\( I(x) = -\log_2(P(x)) \)，其中 \( P(x) \) 是事件 \( x \) 发生的概率。 2. 熵（Entropy）是对随机变量所有可能取值信息量的平均，它衡量了随机变量不确定性。熵的计算公式为：\( H(X) = -\sum_{x \in \mathcal{X}} P(x) \log_2(P(x)) \)，其中 \( H(X) \) 是熵，\( \mathcal{X} \) 是随机变量 \( X \) 的所有可能取值集合，\( P(x) \) 是对应的概率。熵越大，表示随机变量的不确定性越高。 例如，一个有8种等概率取值的随机变量，其熵为 \( \log_2(8) \)。如果这些取值的概率不均等，熵的计算会根据各概率值变化，反映出分布的均匀性。 3. 在分类任务中，交叉熵损失函数通常分为对数似然损失（Log-Likelihood Loss）和对数损失（Log Loss）。当模型需要预测多个类别的概率时，通常采用多类交叉熵损失函数。对于二分类问题，可以使用二元交叉熵损失（Binary Cross-Entropy），而对于多分类问题，则使用多类交叉熵损失（Multiclass Cross-Entropy）。 4. 二元交叉熵损失用于二分类问题，计算公式为： \[ L = -\left[y \cdot \log(p) + (1-y) \cdot \log(1-p)\right] \] 其中，\( y \) 是实际标签（0或1），\( p \) 是模型预测该样本属于正类的概率。 5. 多类交叉熵损失则扩展到多个类别的情况，每个类别都有相应的预测概率，计算公式为： \[ L = -\sum_{c=1}^{C} y_c \cdot \log(p_c) \] 其中，\( C \) 是类别总数，\( y_c \) 是实际标签向量，\( p_c \) 是模型预测第 \( c \) 类的概率。 6. 交叉熵损失函数在训练神经网络时，作为优化目标，通过反向传播算法更新网络参数，以最小化损失，从而提高模型预测的准确性。它能够有效地指导模型学习，尤其是在深度学习模型中，因为其对错误的敏感性使得模型能够快速调整权重。 交叉熵损失函数在人工智能，尤其是机器学习和深度学习中扮演着核心角色，它不仅提供了衡量模型预测性能的标准，还作为优化目标，驱动模型在训练过程中不断学习和改进。通过理解和正确应用交叉熵损失函数，可以有效地解决各种分类问题，提升模型的预测性能。