并行计算在快速多极子方法中的应用

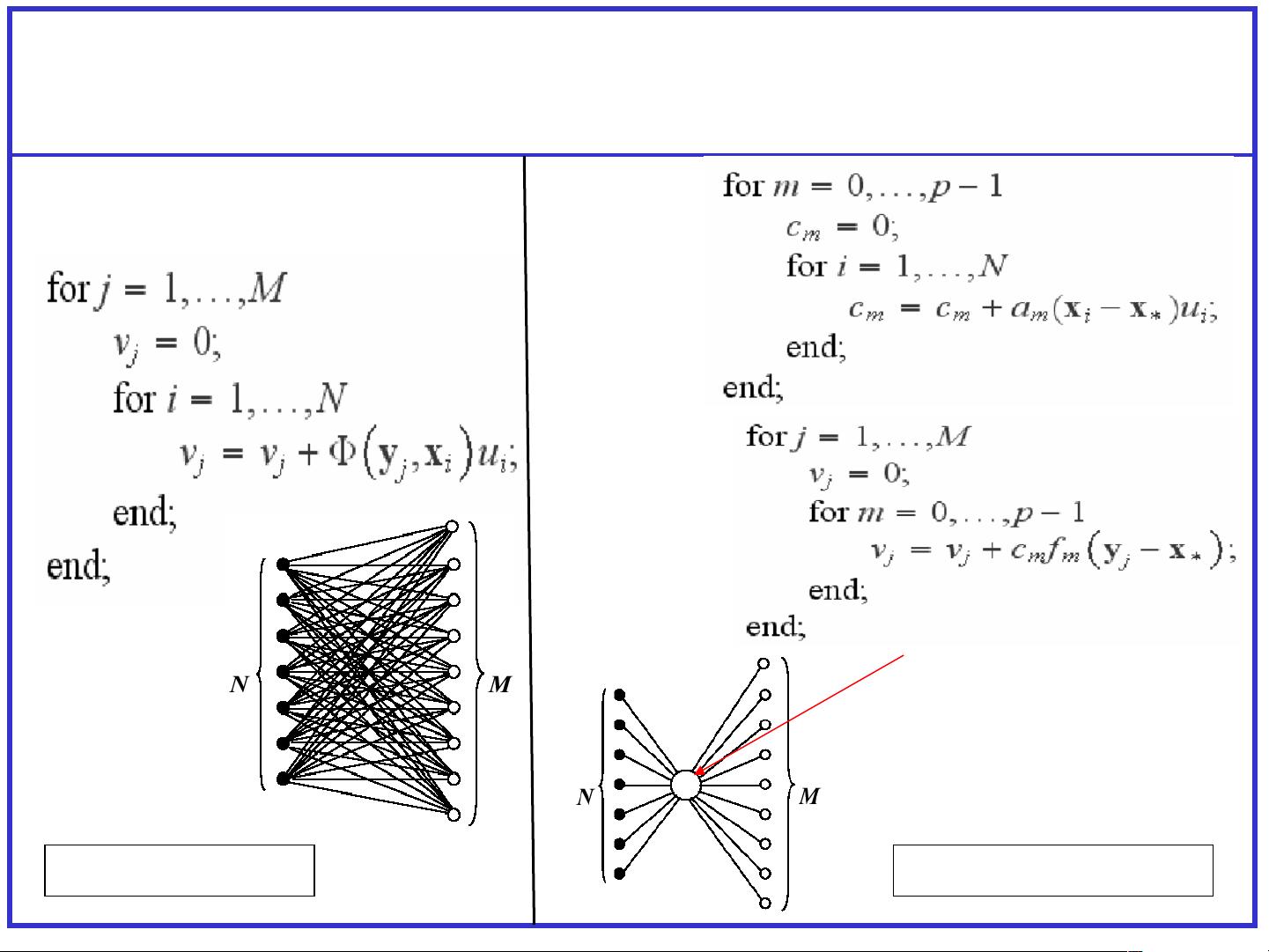
"快速多极子方法的并行技术.ppt" 这篇教学课件主要讨论了在计算电磁学中快速多极子方法（Fast Multipole Method, FMM）的并行化技术。快速多极子方法是一种高效求解大规模电磁问题的数值方法，尤其适用于处理长距离相互作用的问题。它在计算效率上显著优于传统的直接粒子-particle或矩量法，通过将计算任务分解成局部和非局部两部分，大大减少了计算复杂度。 快速多极子方法在电磁场积分方程（如电场积分方程EFIE、磁场积分方程MFIE和混合势边界条件CFIE）中的应用是其核心。这些积分方程基于Green函数来描述电磁场与物体表面的相互作用。例如，Green函数在空间中描述了源点对任意点的场影响，对于解决散射、辐射等问题至关重要。 课件提到了积分方程的离散过程，采用RWG（Rao-Wilson-Glisson）矢量基函数进行离散，这是常用的边值问题离散方法。MOM（Method of Moments）则是将积分方程转化为代数方程组的一种常用技术，通过对物体表面进行网格划分，用RWG函数作为测试函数和插值函数，构建矩阵关系，并最终求解该线性系统。 并行化是提高FMM计算效率的关键。数据结构的设计对并行性能有很大影响，可能涉及如何高效存储和操作多级多极展开，以及如何有效地在不同计算核心之间分配和通信数据。课件中虽然没有详细展开，但通常并行化策略包括数据分区、负载均衡、并行化多级结构的构建和更新等。 在大规模并行计算研究中，可能会使用到分布式内存系统（如MPI）或者共享内存系统（如OpenMP）实现并行，也可能会结合GPU等加速设备进行计算加速。并行化的目标是最大化利用硬件资源，减少计算时间，同时保持计算精度。 这个课件提供了快速多极子方法在并行计算环境下的基本框架，涵盖了理论基础、离散化步骤以及并行化的潜在策略，是深入理解FMM并行技术的一个良好起点。对于学习者来说，进一步研究可能涉及阅读相关的算法细节、并行编程技术和具体的应用案例。