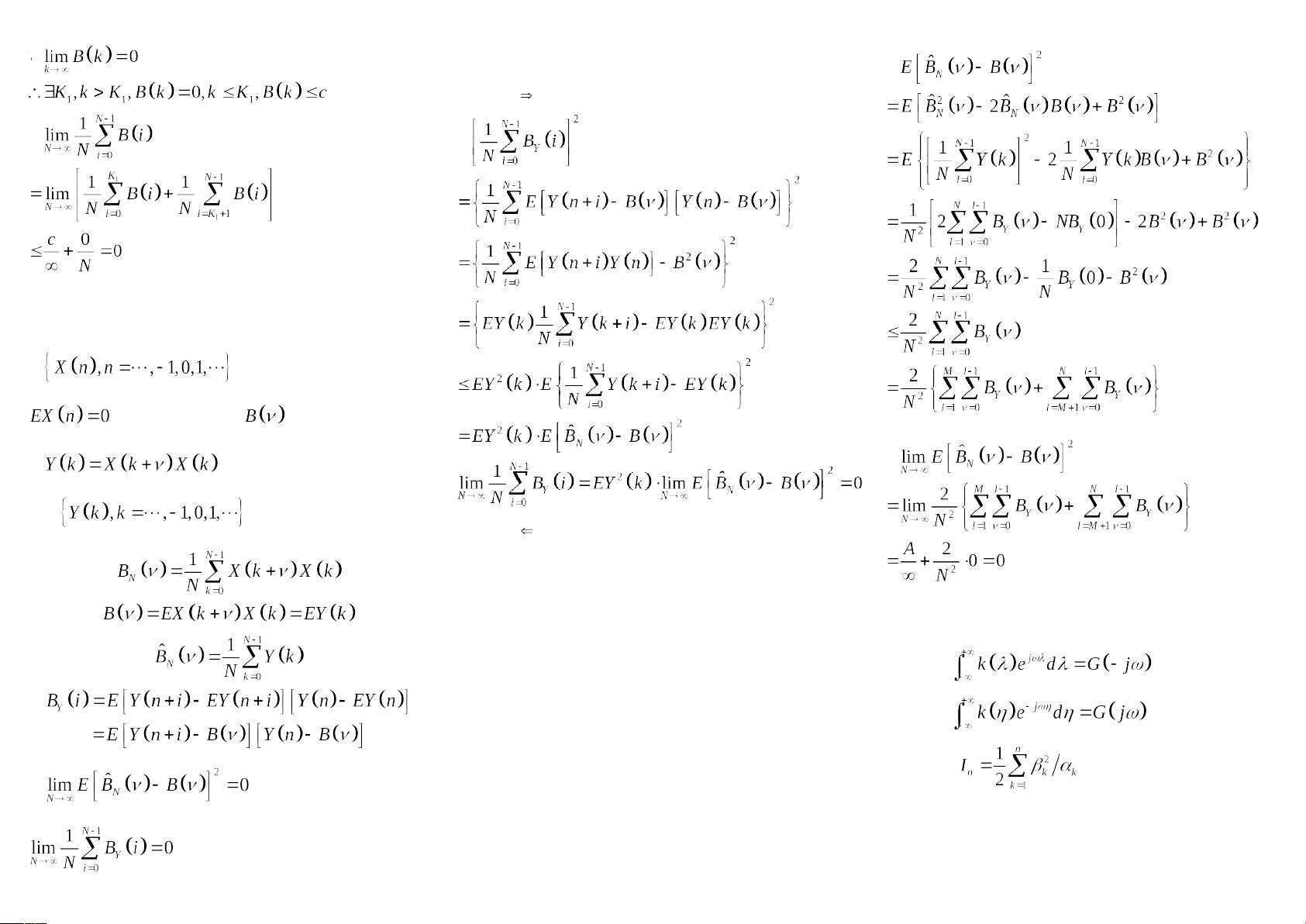哈尔滨工程大学随机过程课程解答与教材问题解析

"哈尔滨工程大学随机过程课程相关的课后习题解答，包括教材《随机过程基础及其应用》和《工程随机过程》的相关内容，涉及历年试题及部分习题详解。" 随机过程是概率论在时间序列分析中的一个重要分支，它研究的是随机变量序列随时间演变的规律。在哈尔滨工程大学的这门课程中，学生需要掌握随机过程的基本概念、性质以及应用。主要知识点包括： 1. 随机过程的基础理论：随机过程的定义，如独立增量过程、马尔科夫过程、布朗运动等，以及它们的特性，如独立性、平稳性、遍历性等。 2. 均值和方差：了解随机过程的均值函数和方差函数，如何通过相关函数或协方差函数来描述随机过程的统计特性。 3. 相关函数和谱密度：学习如何利用相关函数分析随机过程的时间相关性，并通过傅里叶变换理解谱密度在频域中的意义。 4. 特殊过程：如泊松过程，其公式推导及其在计数过程中的应用；平稳正态过程，它的统计特性及在滤波器设计中的应用。 5. 许瓦兹不等式：这是一个在概率论中重要的不等式，用于限制随机变量乘积的期望值，对于理解和证明随机过程的性质非常关键。 6. 习题解答：历年试题中包含了对不同章节习题的解答，如习题0.4、1.12、1.4、2.2、2.6、3.3等，这些解答有助于学生深入理解随机过程的概念和计算方法。 7. 定理和引理：例如定理2.5.1、2.5.3、2.5.6，以及引理1.3.1，这些都是随机过程理论中的核心内容，通常涉及到随机过程的性质证明。 8. 错误修正：教材中可能存在印刷错误，如例1.5.6、例2.1.3、定理2.5.1等，学习过程中需要识别并纠正这些错误，以确保对知识的准确理解。 通过这些内容的学习，学生能够掌握随机过程的基本理论，解决实际问题，如信号处理、通信系统分析、金融数学等领域的问题。同时，通过课后习题的解答，可以检验和巩固理论知识，提升解决实际问题的能力。