图的理论与应用：强连通分量、稠密图与稀疏图解析

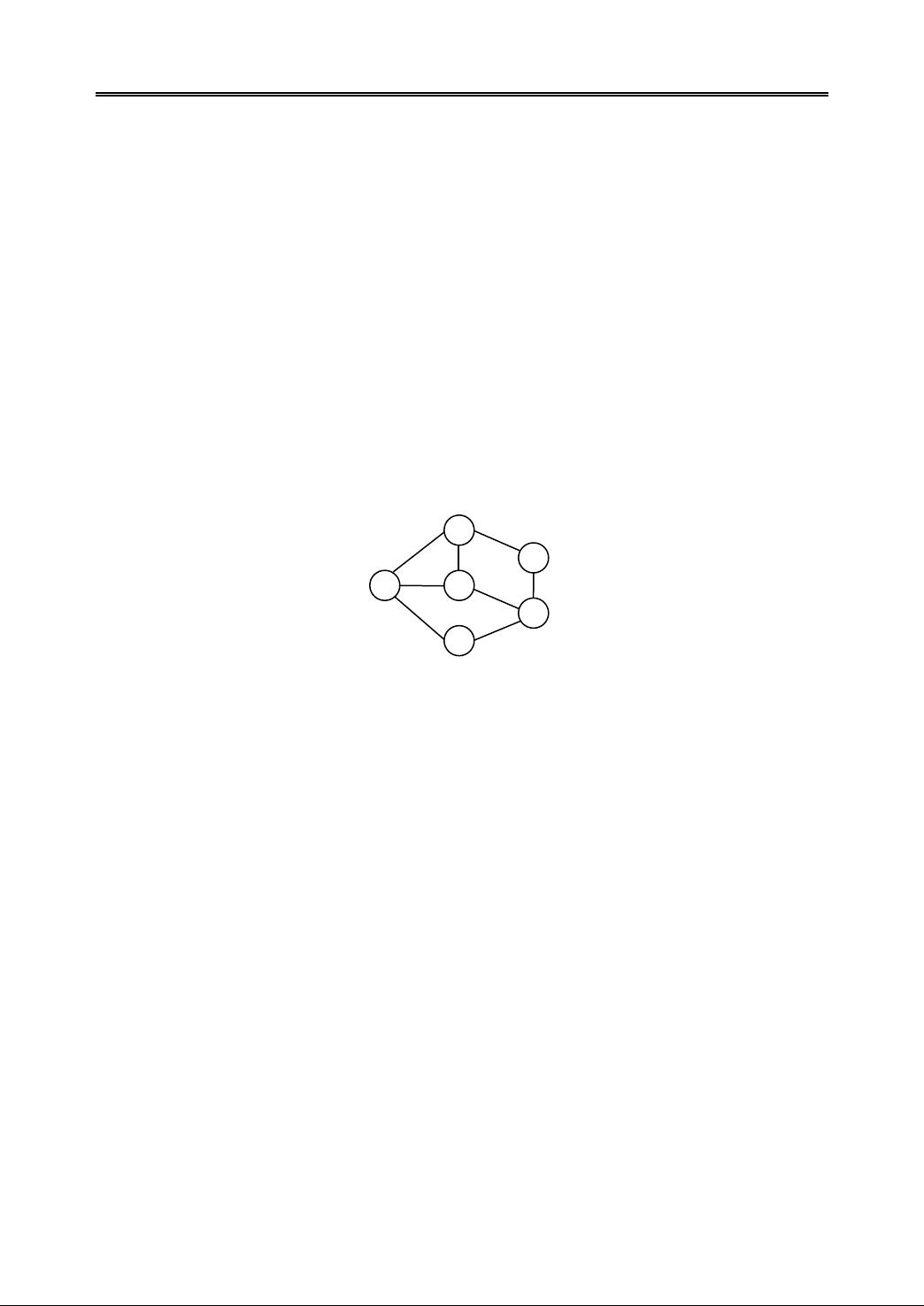
"图的理论与应用" 在图论中，图是一种抽象的数据结构，用于表示对象之间的关系。本章主要探讨了图的相关概念，包括非连通图、连通分量、稠密图和稀疏图，以及邻接矩阵和邻接表这两种常见的图数据结构。 1. **非连通图**：非连通图指的是图中至少存在两个不通过其他顶点互相连接的顶点集合。在给定边数的情况下，要使非连通图的顶点数最少，可以考虑将其分成两个连通分量，其中一个仅包含一个顶点，另一个为完全无向图。例如，一个有28条边的非连通图至少需要9个顶点，其中一个是孤立的，另一个连通分量是一个拥有8个顶点的完全图，因为完全图中每两个不同的顶点间都有一条边，其边数计算公式为n(n-1)/2。 2. **强连通分量**：在有向图中，如果每个顶点都可以通过一系列有向边到达其他任何顶点，则称该子图是强连通的。图8.2（a）展示了一个有向图，其中顶点0、1、2、3、4构成一个强连通分量，而顶点5和6各自构成单独的强连通分量。识别和找出有向图的所有强连通分量是图算法的重要部分。 3. **稠密图与稀疏图**：稠密图是指边数接近于所有可能边数的图（即n*(n-1)/2，其中n是顶点数），而稀疏图则是边数远小于这个值的图。对于稠密图，邻接矩阵作为数据结构较为合适，因为它可以快速查询任意两个顶点之间是否存在边，但空间效率较低。相反，对于稀疏图，邻接表更优，因为它只存储实际存在的边，节省空间，但查询效率稍低。 4. **邻接矩阵和邻接表的使用**： - **求边数**：对于无向图，邻接矩阵中的边数等于1的元素个数除以2；对于有向图，邻接矩阵中的边数等于1的元素个数。邻接表表示时，无论是无向还是有向，边数等于边结点的个数，无向图需除以2。 - **判断两顶点间是否存在边**：邻接矩阵中，元素值为1表示存在边，邻接表中需遍历对应顶点的单链表来确认。 - **计算顶点的度**：对于邻接矩阵，顶点的度等于其对应的行或列中1的个数（无向图是行和列之和的一半）；邻接表中，度等于对应顶点的出度（指向其他顶点的边数）加上入度（被其他顶点指向的边数）。 图论和图数据结构在计算机科学中扮演着核心角色，广泛应用于网络分析、路由算法、社交网络、机器学习等诸多领域。理解并熟练掌握这些概念和操作方法，对于解决复杂问题至关重要。在实际应用中，根据图的特性选择合适的数据结构，能有效提高算法的效率和解决问题的能力。