SPSS多元线性回归分析：汽车特征与销量关系探索

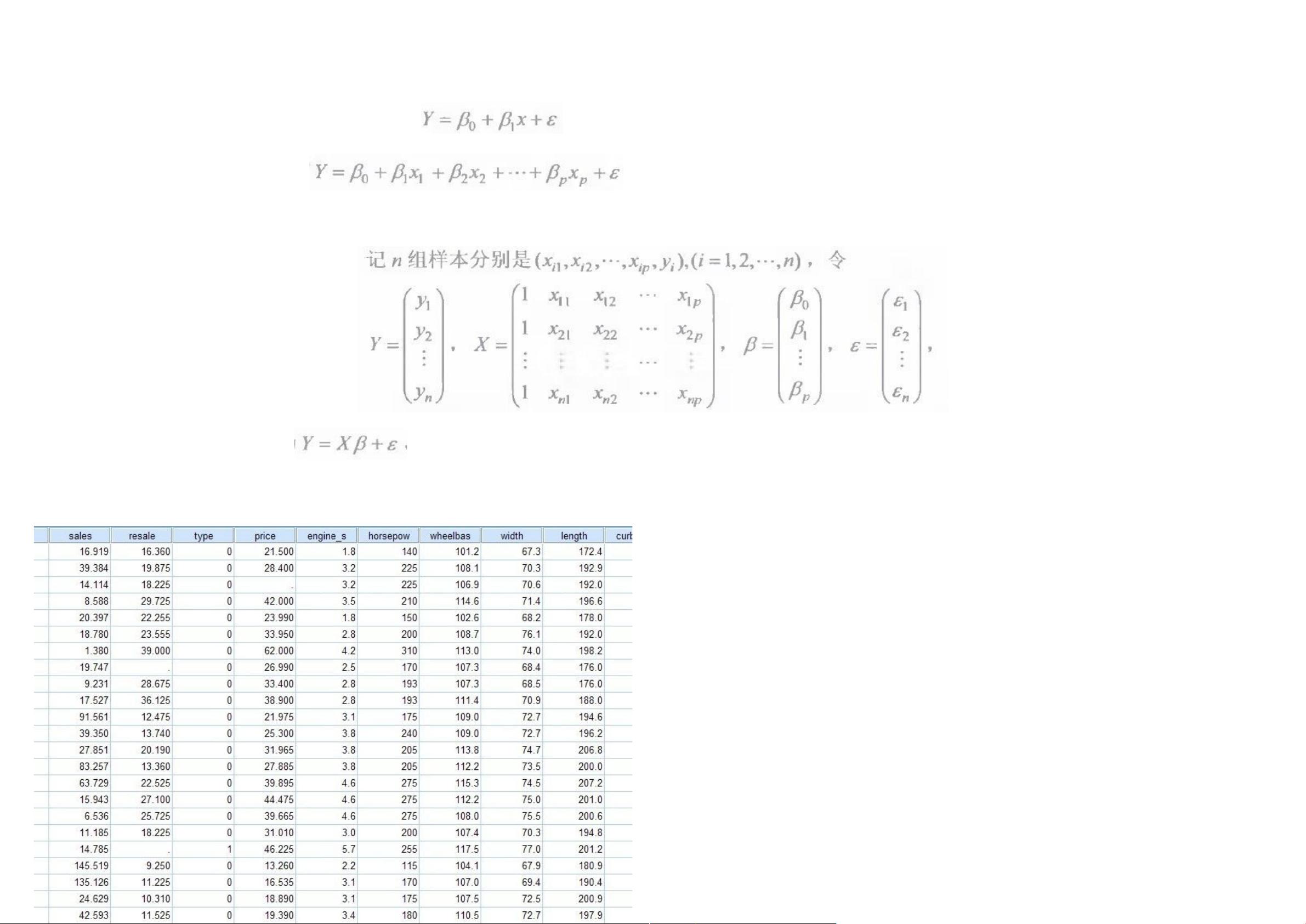
"该文档是关于多元线性回归的实例分析，主要讲解了如何使用SPSS软件进行操作，以分析汽车特征与汽车销售量之间的关系。文档内容包括多元线性回归的基本概念、方程矩阵形式以及随机误差的四个基本假设，并通过实际数据展示了在SPSS中设置回归分析的过程。" 在统计学中，多元线性回归是一种广泛应用的分析方法，用于研究一个或多个自变量（预测变量）与一个因变量（响应变量）之间的线性关系。与一元线性回归不同，多元线性回归考虑了多个可能影响因变量的因素，这使得模型能够更全面地捕捉变量间的复杂关联。 多元线性回归模型可以表示为： \[ Y = \beta_0 + \beta_1X_1 + \beta_2X_2 + \ldots + \beta_pX_p + \epsilon \] 其中，\( Y \) 是因变量，\( X_1, X_2, \ldots, X_p \) 是自变量，\( \beta_0 \) 是截距项，\( \beta_1, \beta_2, \ldots, \beta_p \) 是自变量的系数，而 \( \epsilon \) 是随机误差项。当有 \( N \) 组样本时，这些变量构成一个矩阵，模型以矩阵形式表示： \[ \mathbf{Y} = \mathbf{X\Beta} + \mathbf{\epsilon} \] 其中，\( \mathbf{Y} \) 是因变量的向量，\( \mathbf{X} \) 是自变量的矩阵（包含1作为列的截距），\( \mathbf{\Beta} \) 是系数向量，\( \mathbf{\epsilon} \) 是误差项的向量。 随机误差 \( \epsilon \) 需要满足以下四个关键假设，以保证多元线性回归的合理性： 1. 正态性：误差项服从正态分布。 2. 无偏性：误差项的期望值为0。 3. 同方差性：所有误差项的方差相等。 4. 独立性：误差项之间相互独立。 在SPSS软件中，执行多元线性回归分析通常包括以下步骤： 1. 打开数据文件，将因变量和自变量分别标记。 2. 进入“分析”菜单，选择“回归” -> “线性”。 3. 在弹出的对话框中，将因变量拖入“因变量”框，将自变量拖入“自变量”框。 4. 可以选择不同的方法，如“逐步”或“进入”，来决定自变量进入模型的方式。 5. 设置统计选项，比如选择“回归系数”、“模型拟合度”和“共线性诊断”，以便检查模型的性能和潜在问题。 6. 检查输出结果，分析自变量对因变量的影响程度，以及模型的解释力。 例如，如果选择“逐步”方法，SPSS会基于预设的显著性水平筛选自变量，保留与因变量关系最密切的变量。同时，可以设置额外的筛选规则，对特定自变量进行条件筛选。 通过这些步骤，我们可以得出汽车特征（如车长、车宽、耗油率、车净重等）如何影响汽车销售量的结论，从而建立一个有效的多元线性回归模型，用于预测或解释销售趋势。共线性诊断则有助于识别自变量之间是否存在高度相关性，这可能会影响模型的稳定性。