时变系统辨识与自适应控制作业详解

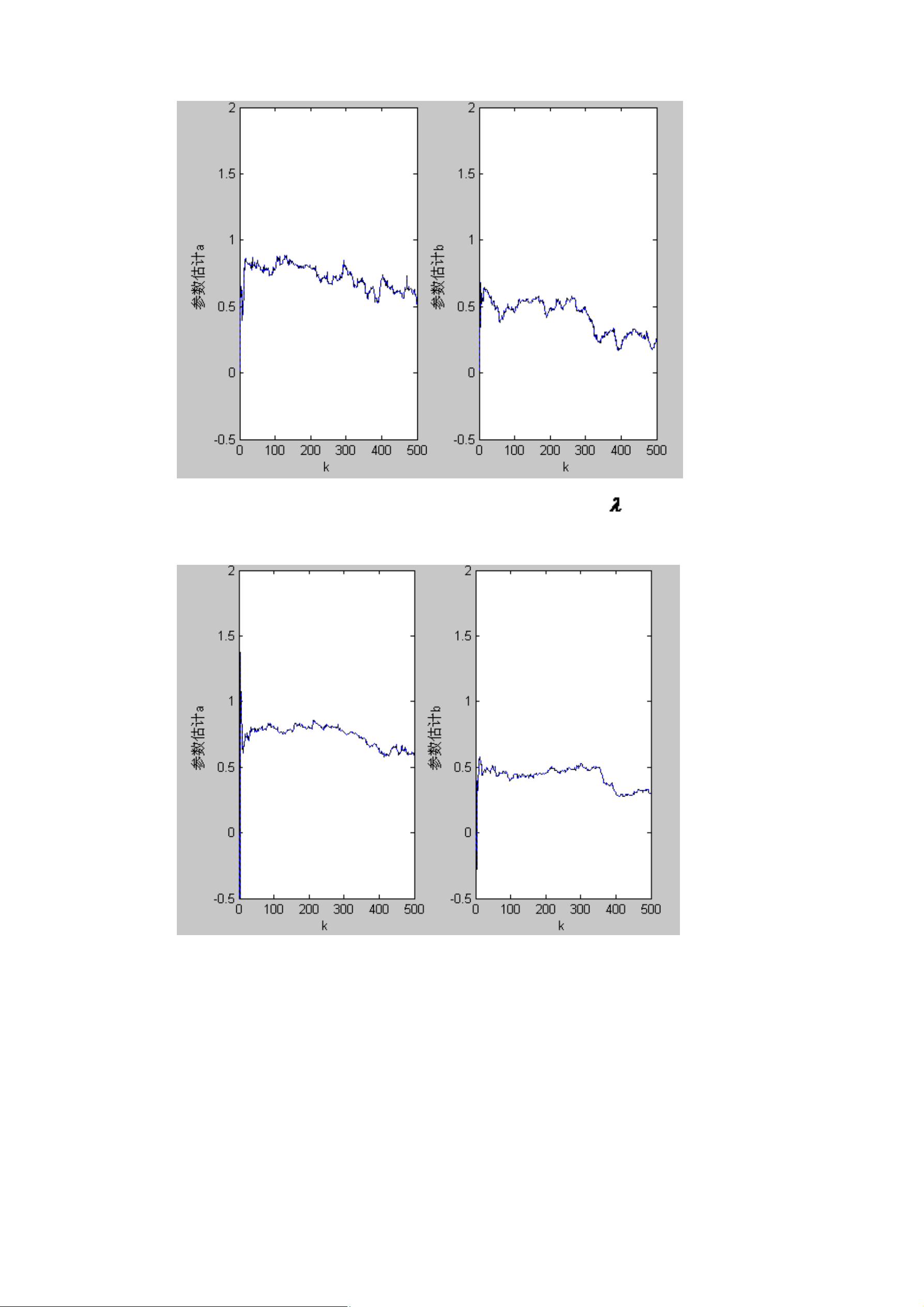
"系统辨识与自适应控制作业探讨了如何在IT领域中进行系统参数估计与控制。首先，作业涉及对时变系统的处理，具体是基于给定的线性动态系统模型y(k)+a(k)y(k-1)=b(k)u(k-1)+e(k)，其中a(k)和b(k)是时变系数，e(k)为零均值噪声。对于定常系统（例如a=0.8, b=0.5），作业要求进行结构确定，即确定系统的阶数，这涉及到分析系统的动力学特性，通常通过观察系统的响应来确定系统的阶数。 接着，作业要求对比分析不同λ值（0.9至0.99）下时变系统辨识的结果和过程。这可能涉及到使用不同的辨识算法或模型，如自适应滤波器或ARMAX模型，来跟踪随时间变化的参数。在λ的变化下，系统的行为可能会有所不同，因此，通过比较不同λ下的识别结果，可以研究系统的动态响应特性以及适应能力。 对于参数估计，作业采用了最小二乘法（LS），这是一种常用的统计方法，旨在找到使测量值与理论预测值之间误差平方和最小的参数估计值。批处理最小二乘法在此处被选择，因为它具有快速收敛和易于理解的优点，适用于处理线性系统参数的估计问题。 作业程序部分展示了如何使用Matlab编程实现参数估计的过程，包括噪声序列的生成、逆M序列的构造、输入信号的更新，以及使用观测数据和模型矩阵构建最小二乘问题的求解。最后，通过计算phi'φ的逆矩阵，得到参数估计值thetae，这是评估系统性能和验证辨识结果的关键步骤。 完成作业后，还需要进行残差检验，即检查估计值与实际值之间的差距，以验证估计的准确性。如果残差过大，可能意味着模型不精确或者存在其他未识别的因素，此时可能需要调整模型或采用更复杂的辨识技术。 这个作业不仅涵盖了系统辨识的基本概念和技术，还涉及到了实际编程操作和统计方法的应用，体现了理论与实践的结合，是IT专业学生深入理解和掌握自适应控制系统的重要实践环节。"