解析连续W+与W-融合：黑洞内非扰动α'修正的新视角

7 浏览量更新于2024-09-03 收藏 371KB PDF 举报

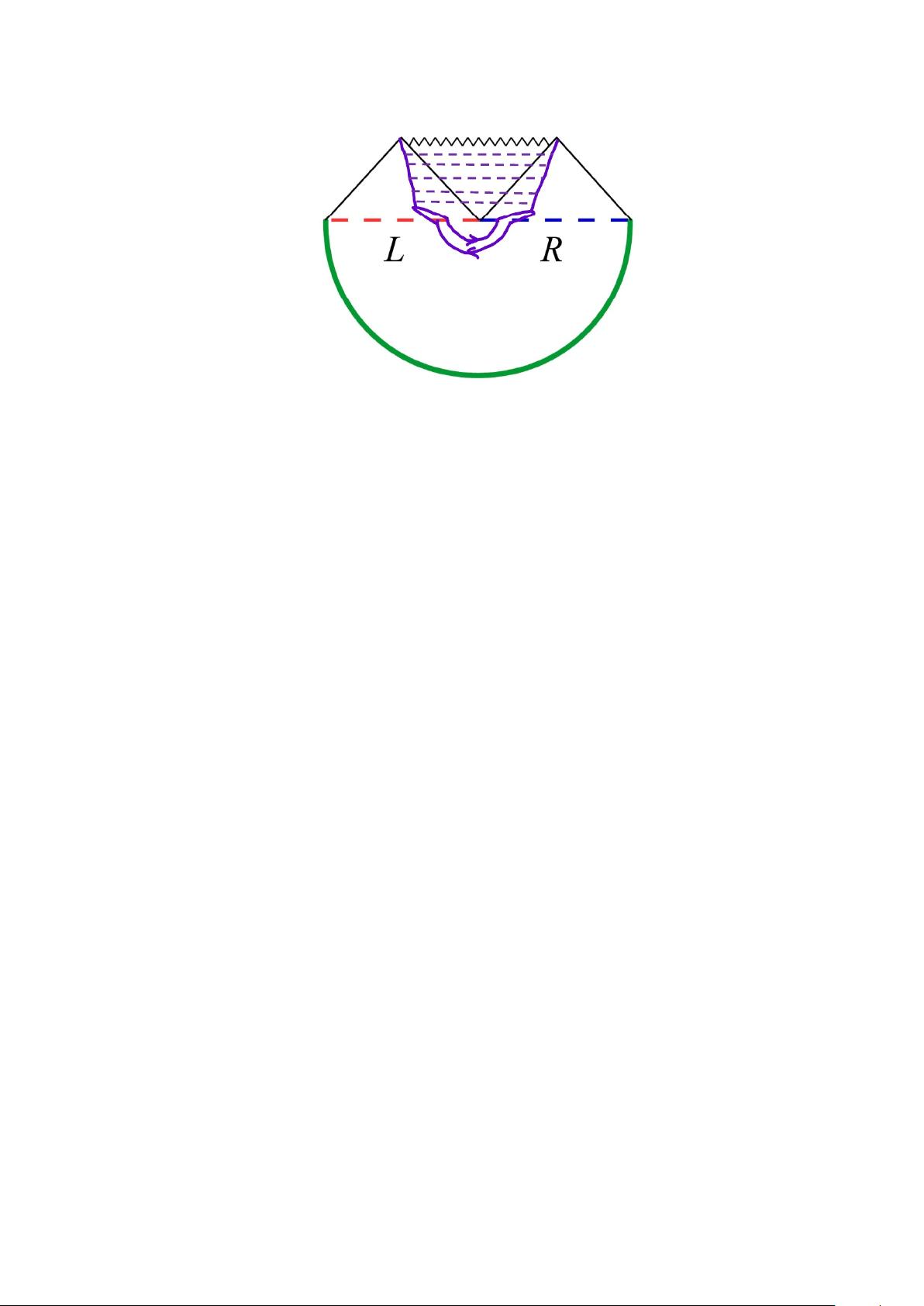
本文探讨了在弦理论背景下，对于Sine-Liouville算子在描述SL(2, ℝ)/U(1)黑洞的非扰动α'校正时所遇到的挑战。通常，这种理论中的α'修正被直观地理解为两个带有不同绕数（Winding number）的弦态的结合，即W+（绕数+1）和W-（绕数-1），它们共同构成了Sine-Liouville算子的表示形式。这个过程在经典弦论中已显示出对雪茄几何（cigar geometry）的有趣影响。然而，在Lorentzian时空中的SL(2, ℝ)/U(1)黑洞中，解析连续的Sine-Liouville算子的凝聚遇到了难题。作者提出了一个新的视角，即在黑洞背景下，非扰动α'修正可以由W+和W-的解析连续融合来描述。这一融合算子旨在解决前者的分析问题，并可能提供了一个新的物理图像：在某种意义上，这个算子代表了折叠的弦，它们填充了整个黑洞，仿佛充当了黑洞内部结构的代理。论文的关键创新在于引入了一个在分析上更为稳健的算子，避免了先前遇到的困难。作者还进行了计算，估算了折叠后的弦的辐射性质，并发现它们以霍金温度进行辐射，这是对黑洞物理学的一个重要贡献。这不仅深化了我们对弦理论中黑洞内部行为的理解，也扩展了我们对量子引力和黑洞熵的认识。总结来说，这篇文章主要关注的是如何在黑洞物理中更好地理解和应用Sine-Liouville算子，特别是在处理非线性效应和量子修正时。通过提出新的算子模型，研究者希望能够揭示更深层次的弦理论与黑洞相互作用的物理机制，从而推动了量子引力理论的发展。

JHEP11(2019)014

Figure 1. The Hartle-Hawking wave function and the non-perturbative α

corrections. In the

Euclidean section there are strings with winding number ±1, denoted in the text by W

. They are

combined in the Lorentzian section to form a folded string, F , that can be viewed as a fusion of

and W

−

BH. If indeed there are classical folded strings inside the BH, then what is the operator in

the SL(2, R)/U(1) coset CFT that describes them?

The aim of this note is to address these questions. We recall [21–24] that, in addition

to (1.2), there is another non-perturbative (1,1) operator, denoted by F , whose underlying

AdS

parent is invariant under the SL(2, R)

×SL(2, R)

current algebra; thus, it condenses.

We argue that it amounts to the BH ﬁlling folded strings. F is not an ordinary vertex

operator; for example, it does not appear to be well deﬁned for generic Q, and the size of

its condensate diverges for Q’s that amount to integer k’s. We show that these problems

are resolved by thinking about F as the fusion of W

and W

−

; schematically,

F ∼ W

∗ W

−

. (1.3)

We are thus led to suggest that, while in the cigar geometry the non-perturbative correc-

tions are described in terms of W

, when we analytically continue to the BH geometry, W

is combined with a W

−

to form an F (see ﬁgure 1), which describes the non-perturbative

corrections in the BH geometry. This is consistent with the fact that F is mutually local

with standard vertex operators in the BH geometry.

The rest of this note is organized as follows. In section 2, we discuss W

and F in

AdS

, and in section 3, we focus on the SL(2, R)/U(1) cigar. In particular, we show that

F is the fusion of W

and W

−

, and sharpen the relation between them both from the

CFT and space-time points of view. Moreover, we propose that while W

is the wave

function of the string condensate, and W

−

its conjugate, their fusion F can be viewed as

the probability density. Section 4 is devoted to the SL(2, R)/U(1) BH. There, we emphasize

the challenge in describing the non-perturbative α

eﬀects using W

, and argue that F

should be identiﬁed with an interior ﬁlling folded string. In section 5, we estimate the

folded string radiation, and ﬁnd it to be thermal with Hawking’s temperature.

– 2 –

剩余13页未读，继续阅读

weixin_38521169

粉丝: 10
资源: 995

解析连续W+与W-融合：黑洞内非扰动α'修正的新视角

不对称内饰，小黑洞

S系内饰带灯条 有图 S系内饰带灯条 有图

自动驾驶时代的内饰变革 延锋汽车内饰推出内饰概念车ID16.pdf

蒸汽清洁内饰

MB-内饰

舒适的内饰

汽车内饰企业网页模板

H5 360度汽车内饰展示

汽车内饰材料的燃烧特性

毕业设计汽车内饰企业应用

最新资源

S系内饰带灯条有图 S系内饰带灯条有图

自动驾驶时代的内饰变革延锋汽车内饰推出内饰概念车ID16.pdf