时间序列分析：趋势模型与估计方法

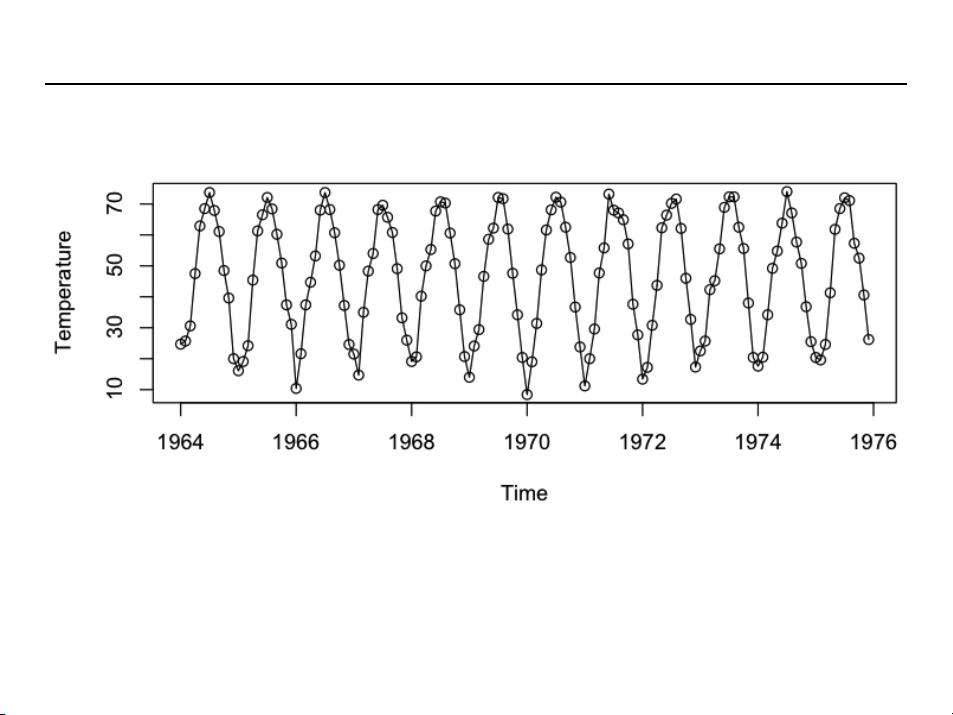
"这是一份研究生级别的《时间序列分析》讲义，由张朝玉副教授主讲，旨在满足多领域学生和研究者对时间序列分析的学习需求。讲义详细介绍了时间序列分析中的趋势分析，包括确定性趋势和随机趋势的概念，并深入探讨了常数均值的估计、回归方法以及残差分析等关键内容。" 时间序列分析是一种统计方法，用于分析和预测按时间顺序排列的数据序列。这份讲义主要关注趋势分析，这是时间序列分析的核心部分，有助于理解和预测数据的长期行为。 在第三章中，张副教授首先区分了确定性趋势和随机趋势。确定性趋势是指数据序列中存在的可预见模式，如线性、二次或周期性趋势。这些趋势可以通过数学模型进行精确描述，例如，迪比克市月平均气温的周期性趋势就归因于地球公转。 随机趋势，如随机游动序列，其特征是序列在任何时间点的均值为零，方差随时间递增。这种类型的趋势不呈现明显的规律性，但可能显示出上升或下降的假象。随机游动模型通常表示为Yt = e1 + e2 + ... + et，其中et是独立且同分布的随机变量。 接着，讲义进入常数均值的估计，这是时间序列分析的基础。当数据序列具有常数均值（不随时间变化）时，可以使用样本均值(¯Y)作为总体均值(µ)的无偏估计。样本均值的计算公式是将所有观测值相加然后除以观测数，其方差可以通过计算自相关函数ρk来估计。如果假设Xt是零均值且平稳的，那么样本均值将有效地捕获数据的中心趋势。 此外，讲义还涉及回归方法，这是估计趋势的一种常用技术。回归估计考虑了数据之间的依赖关系，可以帮助确定趋势项与时间的关系。其可靠性和有效性评估涉及统计检验，如残差分析，该分析检查模型残差是否符合期望的随机性特征，如零均值和无自相关性。 通过这一系列内容，学习者不仅可以理解时间序列的基本概念，还能掌握实际应用中的关键分析技术，如趋势建模、估计和诊断。对于进行经济预测、市场分析、气候研究等领域的研究人员来说，这些都是至关重要的技能。