使用Xilinx FPGA实现数字预失真(DPD)技术

5星 · 超过95%的资源需积分: 50 143 浏览量更新于2024-07-30 5 收藏 3.1MB PDF 举报

"Xilinx DPD (Digital Predistortion) 技术文档，主要应用于消除功率放大器在传输宽频信号时产生的非线性效应。该文档以Xilinx XAPP1128(v1.0)的形式发布，适用于3G移动技术及更高级别的基站。" 在无线通信系统中，功率放大器（PA）在放大信号以增强传输功率的同时，可能会引入非线性失真。这些非线性效应，特别是在传输宽带信号时，会降低信号质量，影响通信系统的性能。为了克服这个问题，"Digital Predistortion (DPD)"技术应运而生。DPD的基本原理是在信号进入功率放大器之前，预先对信号进行逆向失真处理，从而在放大后抵消非线性失真，确保信号的纯净度。 Xilinx的文档详细介绍了如何利用其FPGA（Field-Programmable Gate Array）实现高效的DPD解决方案。FPGA因其可编程性和强大的数字信号处理能力，成为实现DPD的理想平台。文档中提供了一个完整的功能性IP内核描述，这个内核设计用于与3G及更高代际的基站系统配合工作。测试结果是在Axis Common Digital Radio System-Xilinx edition, 2nd edition (CDRSX2)平台上进行的。这是一个硬件-软件协同设计的系统，它充分利用了Xilinx FPGA的数字信号处理特性以及嵌入式处理能力。通过在商用微波PA上执行测量，文档展示了DPD设计的有效性，证明了FPGA在实现DPD功能上的优越性。此外，文档还可能涵盖了DPD算法的实现细节，如模型选择、参数优化、实时校准方法以及与FPGA硬件接口的设计考虑。DPD算法通常基于数学模型，如多项式或记忆多项式模型，以预测和补偿PA的非线性行为。这些模型的复杂度和精确度直接影响到DPD的性能。这份Xilinx DPD文档为设计者提供了一套完整的解决方案，帮助他们理解和实现基于FPGA的DPD系统，以提升通信系统的整体质量和效率。对于从事无线通信和射频设计的工程师来说，这是一份极具价值的参考资料。

DPD Algorithm and Architecture Design

XAPP1128 (v1.0) March 18, 2009 www.xilinx.com 16

— XILINX CONFIDENTIAL — XILINX CONFIDENTIAL — XILINX CONFIDENTIAL

—

The MicroBlaze processor system is configured with 64 kB of internal block RAM memory and

the 32 kB Capture RAM is also reused as working memory after a capture has been

completed. Software has been developed for this platform, which has been comprehensively

tested (see “Performance Testing”). A user interface is provided that allows individual

operational requirements relating to control and monitoring to be met. Details of how to use the

platform and the supplied software is given in “Using the Supplied Software” and “System

Integration.”

At the highest level, the software consists of the following elements:

• Estimation Core Function (ECF) - aligns the transmit and receive data in amplitude, delay,

and phase, and then performs the least-squares estimation. Further details are given in

“Capture Buffers and Estimation Core Function (ECF).”

• Quadrature Modulator Correction (QMC) - aligns the transmit and receive data in

amplitude, delay, and phase, and then computes the Quadrature Modulator errors. Further

details are given in “Quadrature Modulator Correction Algorithm Overview”

• Sample Capture Acceptance (SCA) - uses average power and amplitude histogram

measurement of the capture versus the average signal to ensure that the capture

produces accurate estimation. Further details are given in “Measurements Block and

Sample Capture Acceptance (SCA).”

• Power Amplifier Over-Drive Detection (ODD) - creates a predictive soft metric from the

coefficients computed during ECF indicating when the peaks of the transmitted waveform

are entering the saturation region of the power amplifier. Further details are given in “Over-

Drive Detection Algorithm Overview”.

• Dynamic Control Layer (DCL) – monitors average transmitted power and learns and

applies the coefficients in a manner relevant to the predistortion characteristics of the PA.

Further details are provided in “Dynamic Control Layer (DCL).” The DCL routine can

optionally update the QMC coefficients in a minimally intrusive manner.

Predistorter

The structure implied by Equation 1 is shown in Figure 8, where P

, P

, … are polynomials of

the signal magnitude. It would be very costly in hardware to implement these polynomials

directly. Instead, look-up tables containing 256 complex samples of the polynomials are used.

These are addressed by the complex amplitude of the signal, as indicated by the break-out box

in Figure 8.Testing has shown that this is an adequate number of samples. Further details are

provided in “Sample Rate Datapath.”

X-Ref Target - Figure 7

Figure 7: Xilinx DPD Architecture

Data

Upconverter

Downconverter

DAC

ADC

DUC-CFR

Parameter

Estimator

(MicroBlaze +

RAM)

Capture

Buffer

Measurements

Digital Predistortion Solution

Digital Analog

Observation

Path

Predistortion

Predistortion Sample

Rate

2x Sample Rate

x1044_07_122007

DPD Algorithm and Architecture Design

XAPP1128 (v1.0) March 18, 2009 www.xilinx.com 18

— XILINX CONFIDENTIAL — XILINX CONFIDENTIAL — XILINX CONFIDENTIAL

—

Measurements Block and Sample Capture Acceptance (SCA)

The capture RAM will be able to capture a maximum of approximately 30 μs of data (at 122.88

Msps).

To obtain optimum estimation results, the capture needs to contain data that is representative

of the signal over the lifetime of the coefficients, much longer than the capture length. In

particular, if the capture is taken during a period of time where the signal amplitude is small, for

example, during the low period of a data pulse, the estimation is bad for higher amplitude

signals that might occur over a longer timescale. This is similar in principle to fitting a

polynomial curve to points in a scatter diagram. The function away from the region where there

are data points is an extrapolation yielding unpredictable behaviour.

In some cases, there is a frame structure with a predictably good period that can be used for

estimation. In that case, SCA is not required and instead DPD allows the capture to be

triggered by an external sync pulse, with a programmable delay. WiMAX TDD has such framing

data––the preamble portion of the frame always has the highest power and, with CFR applied

correctly, the highest signal range. Otherwise, the SCA method takes captures at random and

applies acceptance criteria to the samples in the capture RAM to ensure that the samples are

representative of the full signal. Signals are recaptured until one is found that passes these

criteria.

The acceptance criteria are based on the average power and statistics of the transmitted data

in the capture buffers and their comparison to the average power and statistics of the

transmitted signal over a defined measurement interval (typically greater than 10 ms). The

signal statistics are obtained from histograms of the amplitude.

The process is indicated in Figure 10. The Measurements block, as depicted in Figure 7, is

shown in greater detail here. It contains two power meters and two amplitude histogram blocks,

one that runs continuously, with accumulation over a defined measurement interval (typically

10 ms) and one that is a one-shot accumulation over the number of samples to be used for

estimation, synchronized to the sample capture. The software process is symbolized by the

blocks shown on “SW” side of the dotted line.

X-Ref Target - Figure 10

Figure 10: DPD Sample Capture Acceptance Processes

Predistorter

Tx Capture

Rx Capture

Tx Amplitude

PowerHistogram

Power

Histogram

Interval ~10 ms

Accumulation

Capture Length

Accumulation

request

If yes trigger

x1044_10_021908

Measurements Block

Estimation

Capture Meets Target Criteria

Capture Trigger

DPD Algorithm and Architecture Design

XAPP1128 (v1.0) March 18, 2009 www.xilinx.com 19

— XILINX CONFIDENTIAL — XILINX CONFIDENTIAL — XILINX CONFIDENTIAL

—

Dynamic Control Layer (DCL)

The strategy for dealing with average power dynamics, such as would occur via call-load and

power control in a 3G cell site, is driven by the characteristics of a PA when predistorted; that is

precisely what happens when the signal changes (its power for example) after the coefficients

were calculated. These are depicted qualitatively in Figure 11. The key distinguishing feature

among PAs, and one that has a profound effect on the complexity of the DPD solution, is

whether a single coefficient set can be applied over the range of signal powers that are

transmitted. Where this is the case, then once this coefficient set is found it does not need to be

adapted when the transmitted power changes. Amplifiers exhibiting this behavior may be said

to have quasi-static non-linearity (QSNL). Amplifiers that cannot be effectively predistorted over

power dynamics with a single coefficient set may be said to have non-static non-linearity

(NSNL).

Figure 11 is a plot of adjacent channel power (ACP) versus total transmitted power. ACP is a

convenient single numerical measure of spectral compliance. For example, in the 3GPP

TS25.141 transmit spurious requirements, it is required to transmit less than -13 dBm in a

1 MHz wide band offset by 4 MHz from the carrier; this is shown by the Spec line in Figure 11.

Examine the Est@P

max

(green curve). The point at P

max

represents the ACP when the

coefficients of the predistorter are estimated while maximum power is being transmitted. The

correction achieved is the distance to the without predistortion curve.

It should be noted that these curves are obtained when the transmitted power is varied by

changing the digital gain of the signal before predistortion. It is assumed that the analog gain is

fixed. Indeed, predistortion performance is very sensitive to the analog gain after DPD

(because that affects the accuracy of the transfer characteristic model) and, in practice, the

analog gain drifts and should be tracked, as discussed in the following section. It should be

emphasized that the DPD solution here is not intended to be used in any system having fast

analog power dynamics, except in the case of a TDD system where the amplifier can be turned

off during uplink periods to no ill effect.

X-Ref Target - Figure 11

Figure 11: Predistortion Characteristics

ACP

Transmitted Power

Without

Predistortion

Spec

max

min

Est @ Pmax

Est @ P1

Est @ P2

QSNL

NSNL

x1044_11_122007

DPD Algorithm and Architecture Design

XAPP1128 (v1.0) March 18, 2009 www.xilinx.com 20

— XILINX CONFIDENTIAL — XILINX CONFIDENTIAL — XILINX CONFIDENTIAL

—

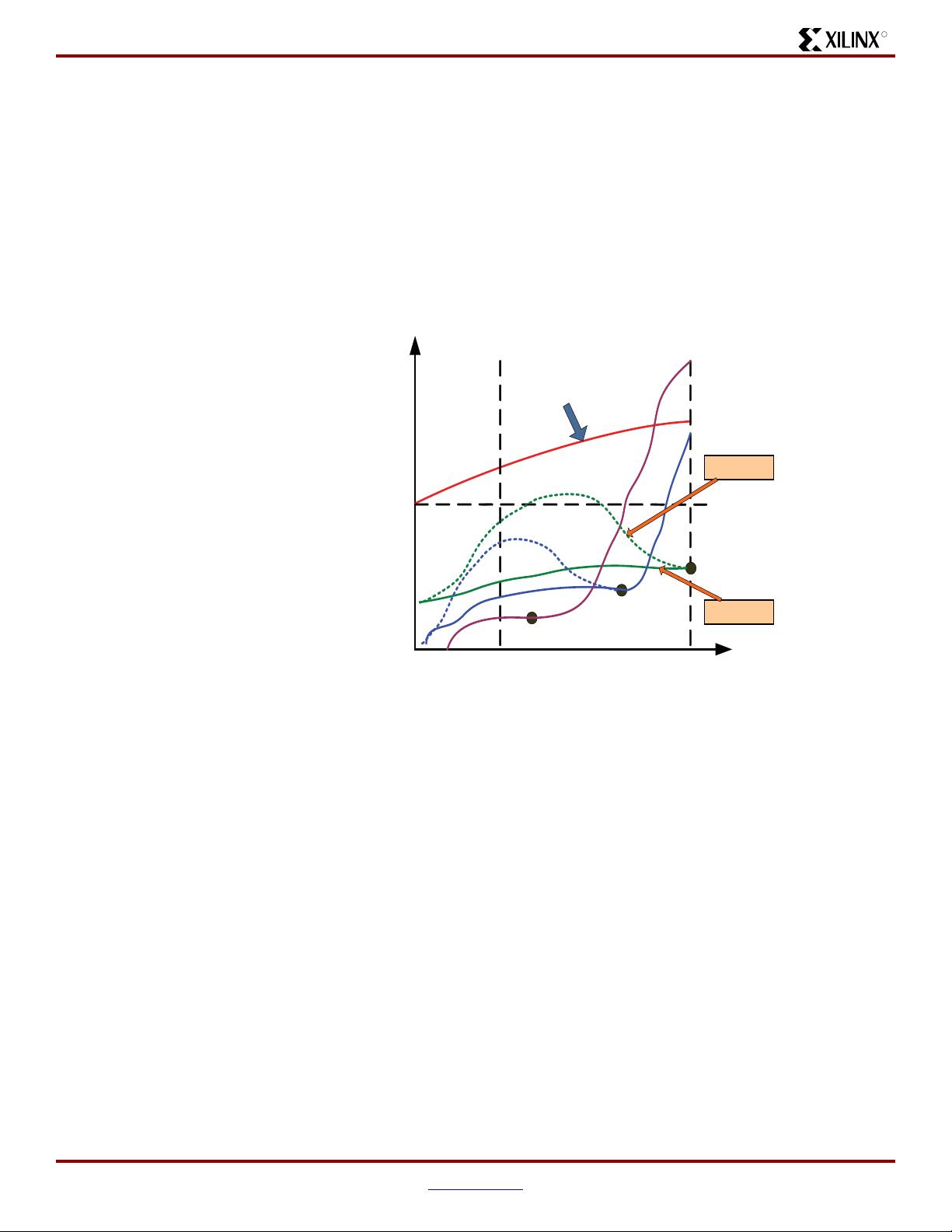
The solid curves show the behavior of a QSNL amplifier. The ACP never crosses the spec line

for any power below the power of the signal at estimation. With coefficients estimated at P

max

the correction remains good for all powers. That is to say, once the coefficients have been

estimated at P

max

, they do not need to be updated––not at least in response to power changes.

They need to be updated to track gain and temperature drift. Now, in an actual deployment, the

power is varying due to the traffic load. Therefore, the P

max

curve may not be immediately

available for coefficient estimation and it is necessary to know what happens if less than P

max

is used for estimation. This is represented by the curves Est@P

and Est@P

, which show that

the coefficients are good for all powers less than the power at estimation, but as the transmitted

power rises above the power at estimation, the spectrum soon goes out of bounds. And for low

powers at estimation time, the ACP performance may be worse with no predistortion at all when

max i

is reached.

This behavior is essentially empirical but is also related to the fact that the

signal range at estimation time is not sufficient for the least-squares solution to be accurate for

the higher powers.

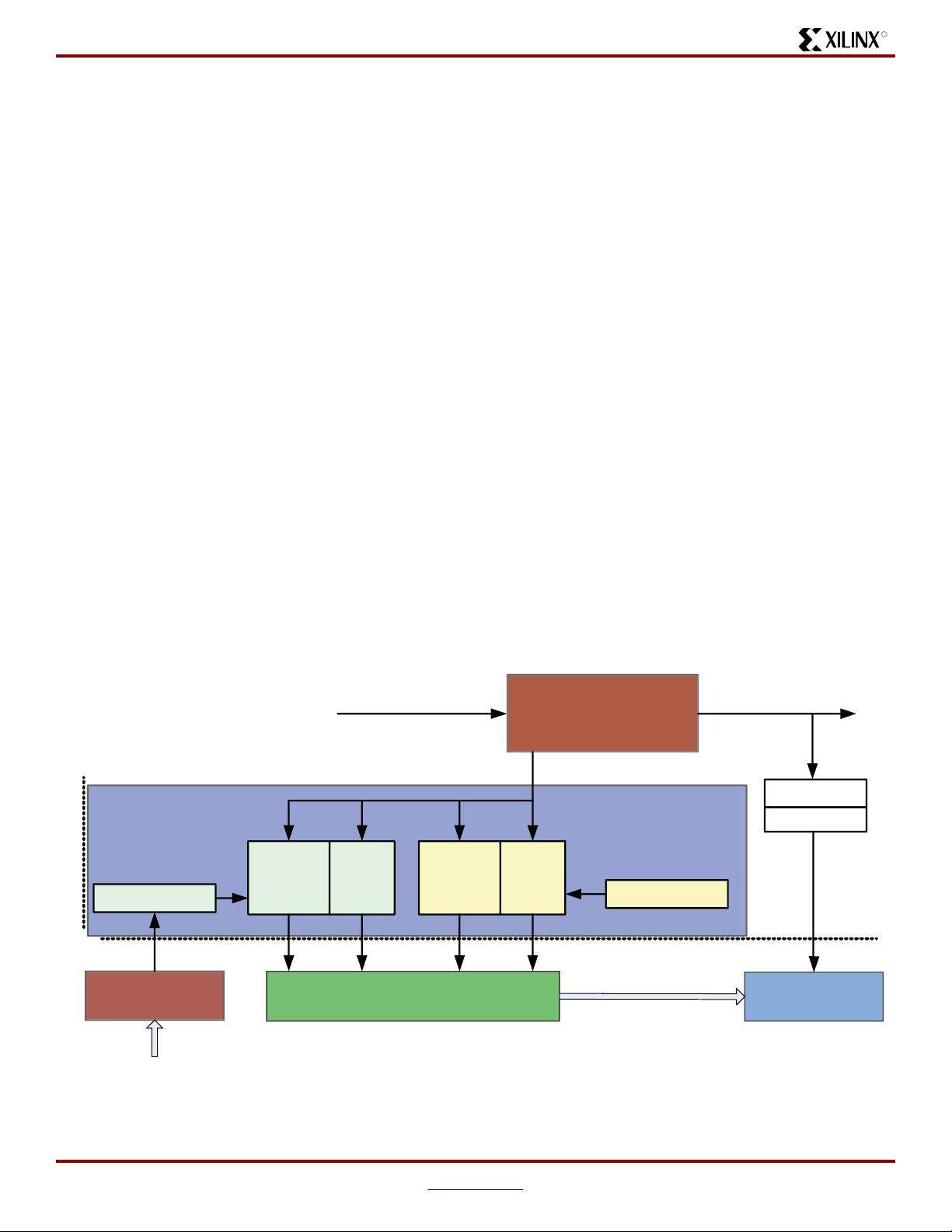
DCL for QSNL Amplifiers

The previous considerations imply an update strategy for QSNL amplifiers, that is, to get on the

max

curve as soon as possible, but also to track analog gain and temperature drift (the

processes occur over timescales like tens of seconds). It is a triggered update, based on the

power measurement.

The method is to store the coefficients used for predistortion together with a record of the power

at which they were estimated (P

est

), then estimate and replace the coefficients whenever the

current measured power (P) crosses a specific threshold. With traffic dynamics, P

est

becomes

closer and closer to P

max

if the trigger is P > P

est

. However, to track analog gain drift it is

necessary to ensure that the predistortion coefficients are unconditionally recalculated within a

certain timespan. Therefore, the trigger condition needs to be modified to allow for situations

when P falls below P

est

. This is obtained by resetting the trigger threshold to P

est

initially and

whenever an estimation is performed. After the threshold has been reset, it decays with time, at

a user programmable rate. When the threshold falls to P, the coefficients are re-estimated. An

example of the behavior of this algorithm is shown in Figure 87 and Figure 88.

The dynamic performance depends on the signal ramp up rates. If the ramp up is slow, the

coefficients never need to be used for powers greatly above their estimated power and no

spectral violation is observed. If, on the other extreme, the power ramps up instantaneously, the

algorithm does not exhibit optimum predistortion until the coefficients are estimated. However,

this is a one-time effect, as subsequent ramp-ups present no problems. The test results in

“Performance Testing” confirm this.

The worst-case initial convergence time is about 1.7 seconds (the speed of our ECF with

default parameters), which meets the majority of operational needs. To cover cases where this

is a problem, off-air calibration can be performed and optimum initial coefficients can be pre-

loaded.

With QSNL amplifiers, there is no need for fast coefficient update.

剩余157页未读，继续阅读

duoerpu

粉丝: 0
资源: 1

使用Xilinx FPGA实现数字预失真(DPD)技术

DPD火焰监测器（1010）.doc

PG DBA培训文档Ver0.11.pdf

低反馈成本的DPD研究论文

xilinx dpd 资源评估

XILINX DPD v2.0.rar

xilinx dpd (数字预失真）文档

大数定律与中心极限定理在Xilinx DPD文档中的应用实例

Xilinx DPD V3.0 FPGA控制与调试：从基本命令到深入理解

xilinx dpd 2.0 mdl

xilinx dpd (数字预失真)文档

最新资源