张量分解入门：CP与Tucker分解解析

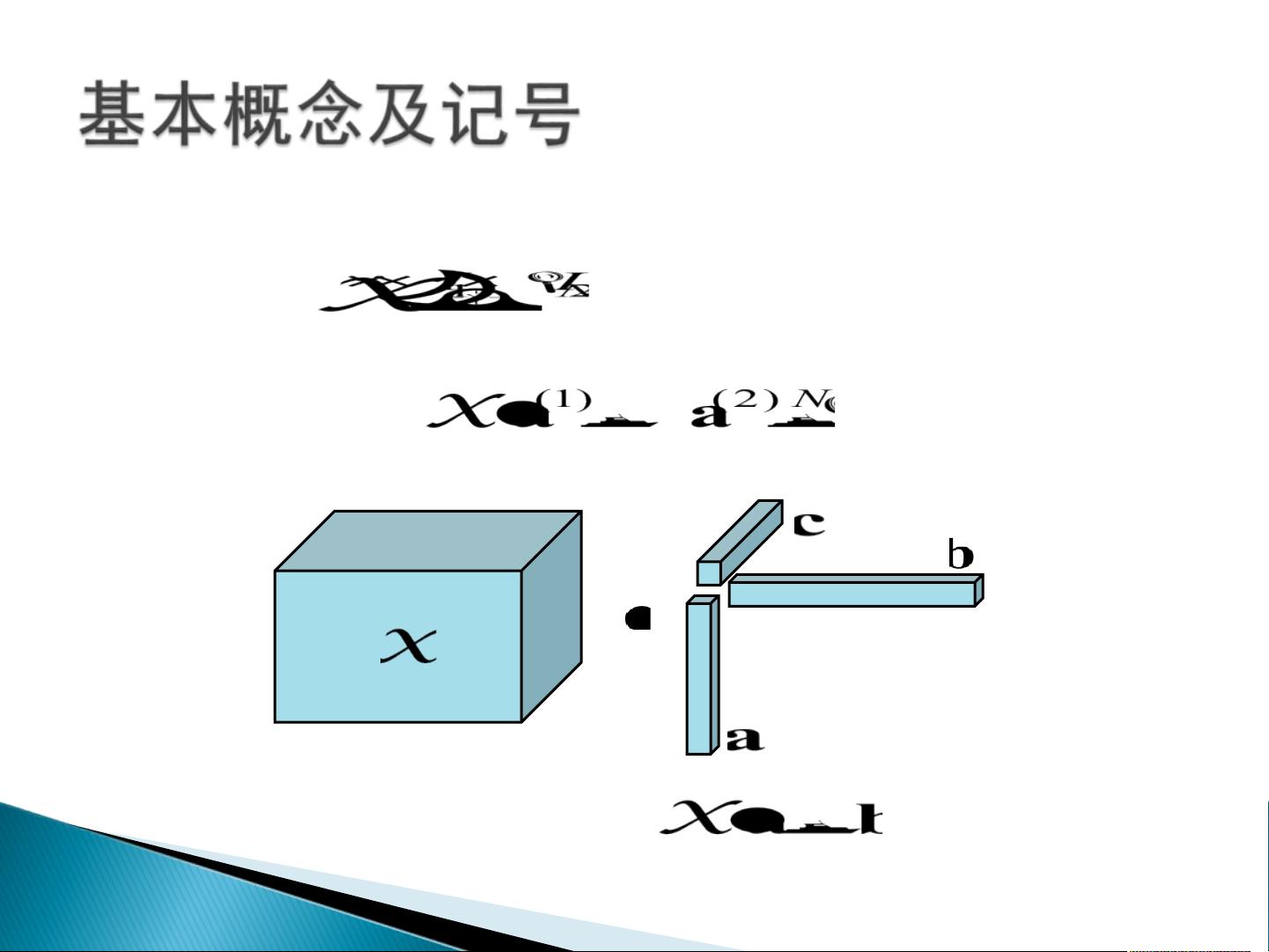
"张量分解是数学和计算领域中处理多维数据的一种重要技术，主要包括张量的CP分解和Tucker分解。这份PPT详细介绍了张量的基本概念、记号、不同类型以及相关的运算，旨在帮助初学者理解张量及其应用。" 在数学中，张量是一种抽象的多维数组，可以被视为向量和矩阵的推广。一阶张量对应于向量，二阶张量对应于矩阵，而三阶或更高阶的张量则代表更复杂的多维结构。张量空间是由多个向量空间基底外积构成的空间，张量的阶定义为构成该空间的向量空间的个数。 张量的纤维是张量在特定模式下的线性组合，比如mode-1纤维对应于列，mode-2纤维对应于行，而mode-3纤维对应于“管”。切片则是将张量沿着特定维度进行切分，例如水平切片、侧面切片和正面切片。 张量的内积和范数是衡量张量之间关系的重要工具。内积定义了两个张量的相似度，Frobenius范数则提供了张量的大小度量。秩一张量是指可以表示为多个向量外积的张量，这在张量分解中至关重要。 CP分解（Canonical Polyadic Decomposition）是一种将高阶张量分解为一系列 rank-1 张量（向量的外积）的线性组合，形式上，一个N阶张量可以表示为N个向量的外积。这种分解有助于揭示数据的潜在结构和模式。 Tucker分解，又称为多线性主成分分析（Multilinear Principal Component Analysis），将高阶张量分解为一个核心张量与一组沿每个模式的因子矩阵的乘积。核心张量捕获张量的全局信息，而因子矩阵则捕获各模式上的局部信息。 张量的对称性和对角性是两个重要特性。对称张量在下标任意排列下保持不变，而超对称张量是更高阶的对称概念，要求在所有可能的下标排列下元素相等。对角张量则意味着只有在特定位置（对应对角线）上的元素非零，其余位置均为零。 展开（matricization或unfolding）是将张量转换为矩阵的过程，这对于将张量方法应用于传统的矩阵算法非常有用，如奇异值分解或主成分分析。 张量分解在数据分析、图像处理、机器学习、信号处理等领域有广泛应用，通过理解和掌握这些基本概念和技术，我们可以更好地处理和理解多维数据集的复杂性。这份PPT提供了一个很好的起点，引导初学者逐步深入到张量理论和应用的世界。