强化学习：4x4网格DP问题分析与实现

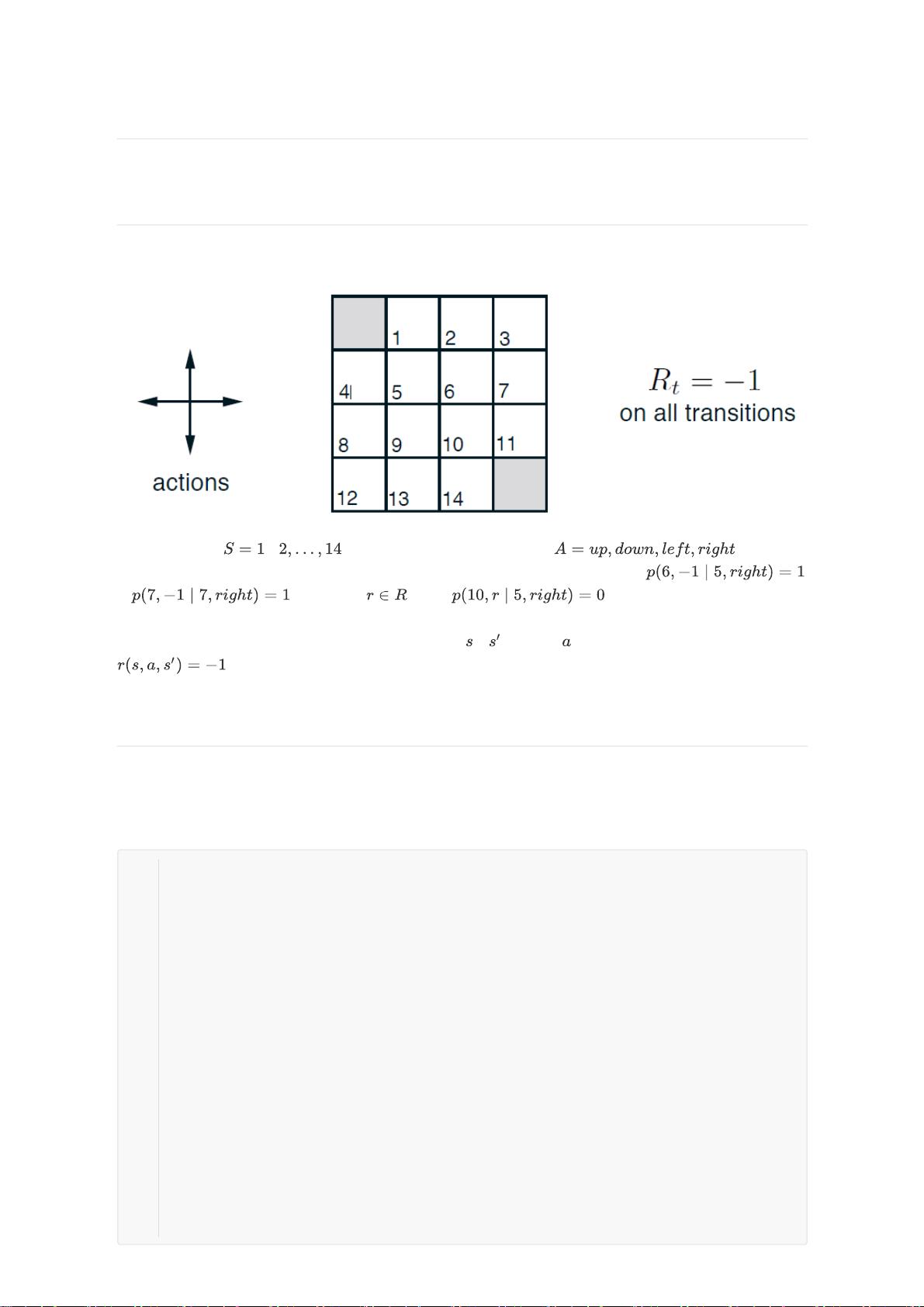
在本资源中，我们探讨了一个基于《强化学习：一个介绍》（Reinforcement Learning: An Introduction）第4章例4.1的问题，这是一个关于动态规划(DP)的小型网格问题。网格图是一个4x4的非终止状态空间，状态可以通过四种动作进行转移：向上、向下、向左和向右。然而，如果动作导致智能体离开网格，状态不会改变。任务是无折扣的分幕式，目标是在未达到终止状态前获取最大累积回报，所有动作的即时奖励都是-1。 问题的核心是计算在采取等概率随机策略下的价值函数序列在迭代策略评估中的收敛情况。环境设置包括以下关键部分： 1. **环境定义**： - 导入必要的库函数，如`matplotlib`和`numpy`，用于可视化和数值计算。 - 定义网格世界大小为4x4，动作包括四个基本移动方向。 - 动作选择的概率均匀分配为0.25，表示智能体在选择动作时等概率执行。 - 设定终止状态为左上角(0,0)和右下角(WORLD_SIZE-1, WORLD_SIZE-1)。 2. **动作执行过程**： - `is_terminal`函数判断当前状态是否为终止状态。 - `step`函数模拟智能体执行动作并更新状态，如果动作导致离开网格，状态保持不变。 3. **辅助函数**： - 用于画图和可视化网格，帮助理解智能体的行为和状态变化。 - 用户策略描述辅助函数可能涉及到策略迭代或值迭代过程中的策略评估和更新。 在解决这个问题时，主要步骤可能涉及构建价值函数表格，初始化所有状态的价值估计，然后根据动作选择概率和环境动态更新这些估计值。通过重复这个过程（例如，使用γ（折扣因子）和ε-greedy策略），我们可以观察价值函数在每次迭代后的收敛趋势，以及智能体如何逐渐学习到最优路径以最大化累积回报。最后，这将有助于深入理解强化学习中的动态规划应用，特别是在没有明确最优策略的情况下，如何通过迭代优化来寻找近似解决方案。