时间序列模型分析：平稳性与预测方法

"本章介绍了时间序列模型的基本概念和分类，包括一元和多元时间序列、离散和连续时间序列、平稳与非平稳时间序列，以及高斯型和非高斯型时间序列。时间序列分析主要关注长期趋势、季节变动、循环变动和不规则变动。常见的模型有加法模型、乘法模型和混合模型。移动平均法是一种用于揭示长期趋势的预测技术，通过计算连续项数的时序平均数。" 时间序列模型是数据分析中的关键部分，它涉及按时间顺序排列并随时间变化的数据序列。根据不同的分类标准，时间序列可以分为： 1. 一元和多元时间序列：一元时间序列专注于单一对象的变化，而多元时间序列则考虑多个相互关联的对象。 2. 离散和连续时间序列：离散时间序列由特定时间点上的数据点组成，而连续时间序列则是在任意时间点上都有数据。 3. 平稳和非平稳时间序列：平稳时间序列的概率分布不随时间改变，其均值和方差保持恒定；非平稳时间序列的统计特性会随时间变化。宽平稳时间序列是统计特性（如均值和协方差）只与时间差有关，而与绝对时间无关的序列。 4. 高斯型和非高斯型时间序列：高斯型时间序列遵循正态分布，而非高斯型时间序列则可能具有其他类型的分布。 时间序列分析包括预测技术，通过分析数据的变化趋势来预测未来的值。常见的趋势变化形式有： - 长期趋势变动：反映事物的持续上升、下降或稳定状态。 - 季节变动：与特定季节相关的周期性变化。 - 循环变动：周期超过一年，非季节性的波动。 - 不规则变动：包括突发性和随机性变化。 时间序列模型通常采用以下类型： - 加法模型：总值等于各成分（趋势、季节性、循环性和随机性）之和。 - 乘法模型：总值等于各成分的乘积。 - 混合模型：结合了加法和乘法模型的特点。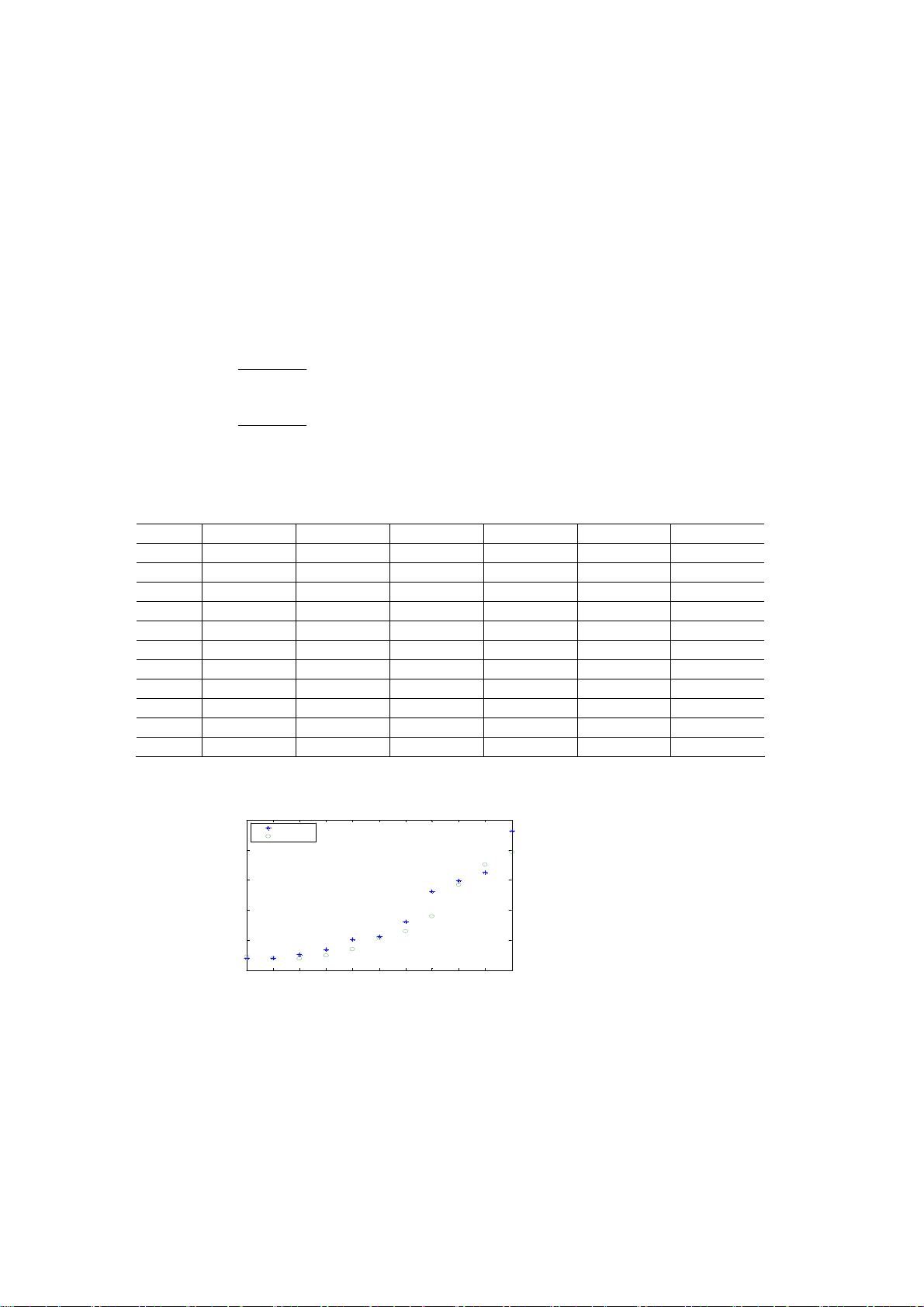 移动平均法是预测长期趋势的一种实用方法，通过计算一段时间内的平均值来滤掉短期波动，揭示出潜在的趋势。这种方法适用于随机变动小、趋势明显且无突然变动的情况。 时间序列模型在理解和预测各种现象，如经济指标、销售数据、股票价格等，有着广泛的应用。通过选择合适的时间序列模型，可以更好地解析数据的内在模式，为决策提供有力支持。