Apollo控制算法深入解析：LQR最优控制

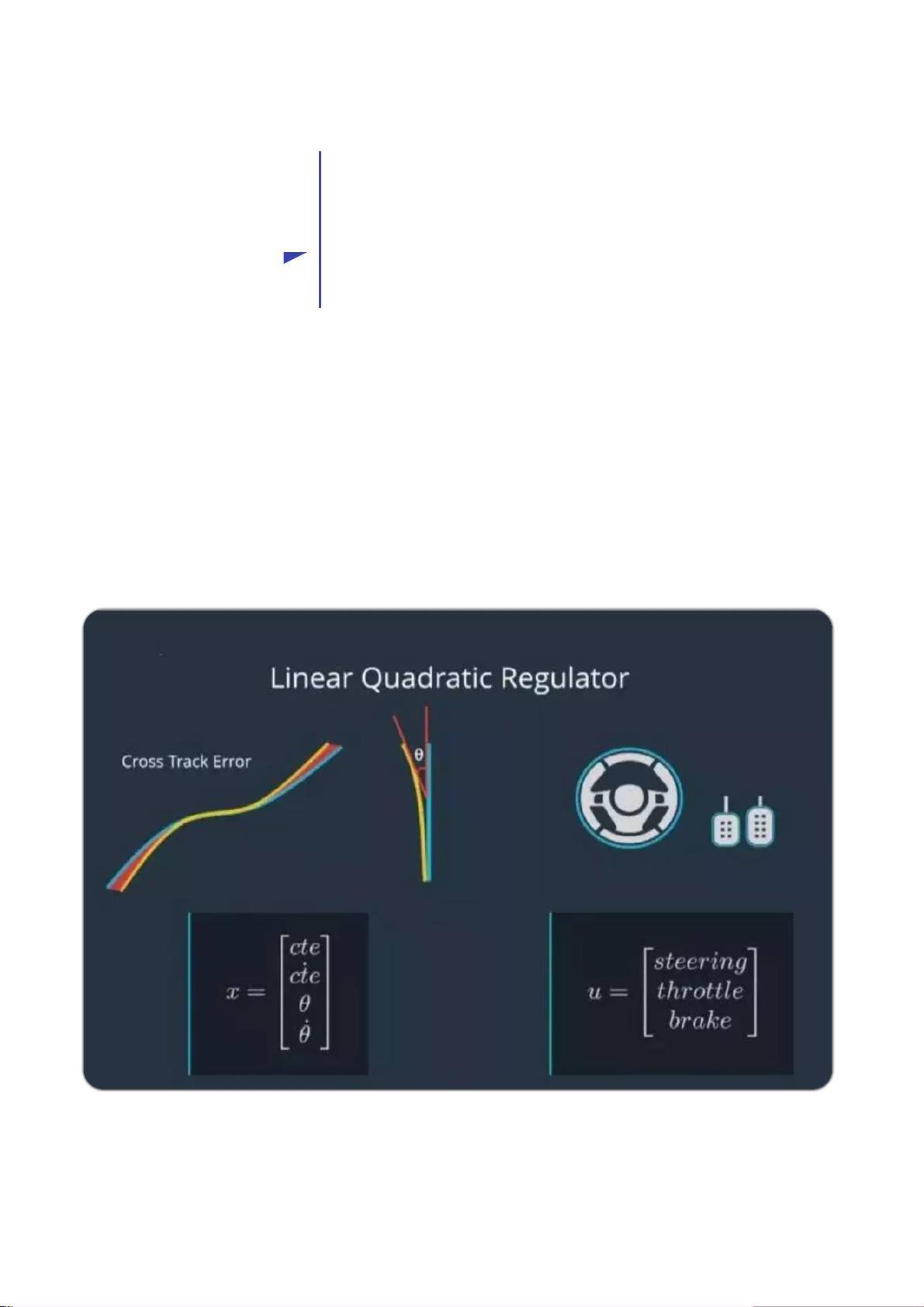
"这篇文档详细介绍了Apollo控制算法中的LQR（Linear Quadratic Regulator），这是一种在自动驾驶领域广泛应用的控制策略。作者是社区开发者卜大鹏，他深入浅出地阐述了LQR的基本理论和推导过程，特别是如何应用于Apollo系统的横向控制。" LQR理论是一种在控制系统设计中广泛使用的最优控制方法，它源于现代控制理论，尤其适用于状态空间表示的线性系统。LQR的目标是找到一个最优的状态反馈控制器，以最小化一个二次型的性能指标，通常表现为系统的状态偏差和控制输入的能量之和。这一最优控制策略能够确保系统的稳定性，并且使得控制代价尽可能小。 在自动驾驶场景中，LQR被用于精确地控制车辆的行驶方向，这包括对横向误差、横向误差变化率、朝向误差以及朝向误差变化率的控制。这些状态变量构成了状态集合X，而车辆可以通过调整转向、加速和制动等控制输入U来影响这些状态。 LQR的设计涉及到权矩阵Q和R的选择，它们分别对应于状态误差和控制输入的权重。Q矩阵决定了系统对状态偏离期望值的敏感程度，R矩阵则反映了对控制输入大小的惩罚。通过调整这两个矩阵，设计师可以平衡控制精度和控制成本。 文档中提到的离散线性系统是LQR理论的基础，其目标是找到一个控制序列，使得系统的状态能以最小的代价转移到期望的最终状态。代价函数J包含了状态x和控制u的二次项，以及到达最终状态的控制序列的总代价。通过对J进行优化，可以找到最佳的控制策略。 动态规划算法在这里发挥了关键作用，通过反向传播的方式，从最终状态开始向前计算每个时间步的最优控制。这涉及到一个递推关系，即当前最优控制的确定依赖于下一个时间步的最优控制。这个关系可以表示为动态规划的Bellman方程，从而将原问题转化为一系列子问题，逐步求解最优控制序列。 通过计算代价函数J的梯度并使其等于零，可以解出控制输入的最优值，这通常是通过求解黎卡提方程来实现的。黎卡提方程是一个与状态空间模型相关的线性常微分方程，它的解可以给出最优控制律的系数矩阵K。 总而言之，Apollo控制算法中的LQR策略是一个精心设计的状态反馈控制方案，它利用现代控制理论中的最优控制原理，结合动态规划方法，以最小化总体成本为目标，实现对自动驾驶车辆的精确控制。这一策略不仅考虑了系统的稳定性，还兼顾了控制效率，是自动驾驶技术中的核心算法之一。