五维标量张量重力中的反de Sitter弦状黑洞解

58 浏览量更新于2024-07-16 收藏 593KB PDF 举报

"这篇文章是关于标量张量重力理论中的新型反德西特（Anti-de Sitter，AdS）膜黑线解的研究。作者Theodoros Nakas、Nikolaos Pappas和Panagiota Kanti在五维理论框架下，探讨了标量场与重力的非最小耦合效应，寻找并解析地解决了描述弦上Schwarzschild-AdS时空的黑线解。他们提出了两种完整解决方案，这两个方案的特点包括规范的标量场、在膜上的局部能量动量张量以及产生空间翘曲的负定非平凡体势。即使没有传统的负大宇宙学常数，这种翘曲也能自我维持。文章指出，当膜上黑洞的质量设为0时，黑线解会消失，留下一个仅在第五维边界有真实奇点的规则膜世界模型。" 这篇研究论文深入探讨了高维理论中的物理现象，特别是五维标量张量重力理论。在这个理论中，一个标量场与重力以非最小耦合方式相互作用，这导致了一些新的物理特性。研究的核心是寻找和分析黑线解决方案，即在反德西特膜（brane）上形成的黑洞状结构。这些解是通过精心选择标量场的非最小耦合函数来解析求得的，它们展示了如何在膜上形成Schwarzschild-AdS时空。值得注意的是，这些黑线解的特性不同于传统的模型。首先，标量场保持规则，避免了通常与黑洞相关的奇异性。其次，能量动量张量在膜上局部集中，暗示着能量密度的特定分布。此外，体势是负定且非平凡的，这意味着它能够独立支撑空间的翘曲，即使没有传统的负宇宙学常数。这揭示了一种新的物理机制，可以产生翘曲效应，而无需依赖通常与AdS空间相关的负宇宙学常数。研究还发现，如果去除膜上黑洞的质量，黑线解会消失，转化为一个无黑线的规则膜世界模型。这个模型只在第五维的边界上有一个真实的奇点，这为理解高维宇宙结构提供了一个新的视角。这篇开放获取的文章为理解五维标量张量重力理论下的黑洞行为和空间翘曲机制提供了新的见解，同时也为探索高维宇宙模型的物理特性提供了有价值的参考。

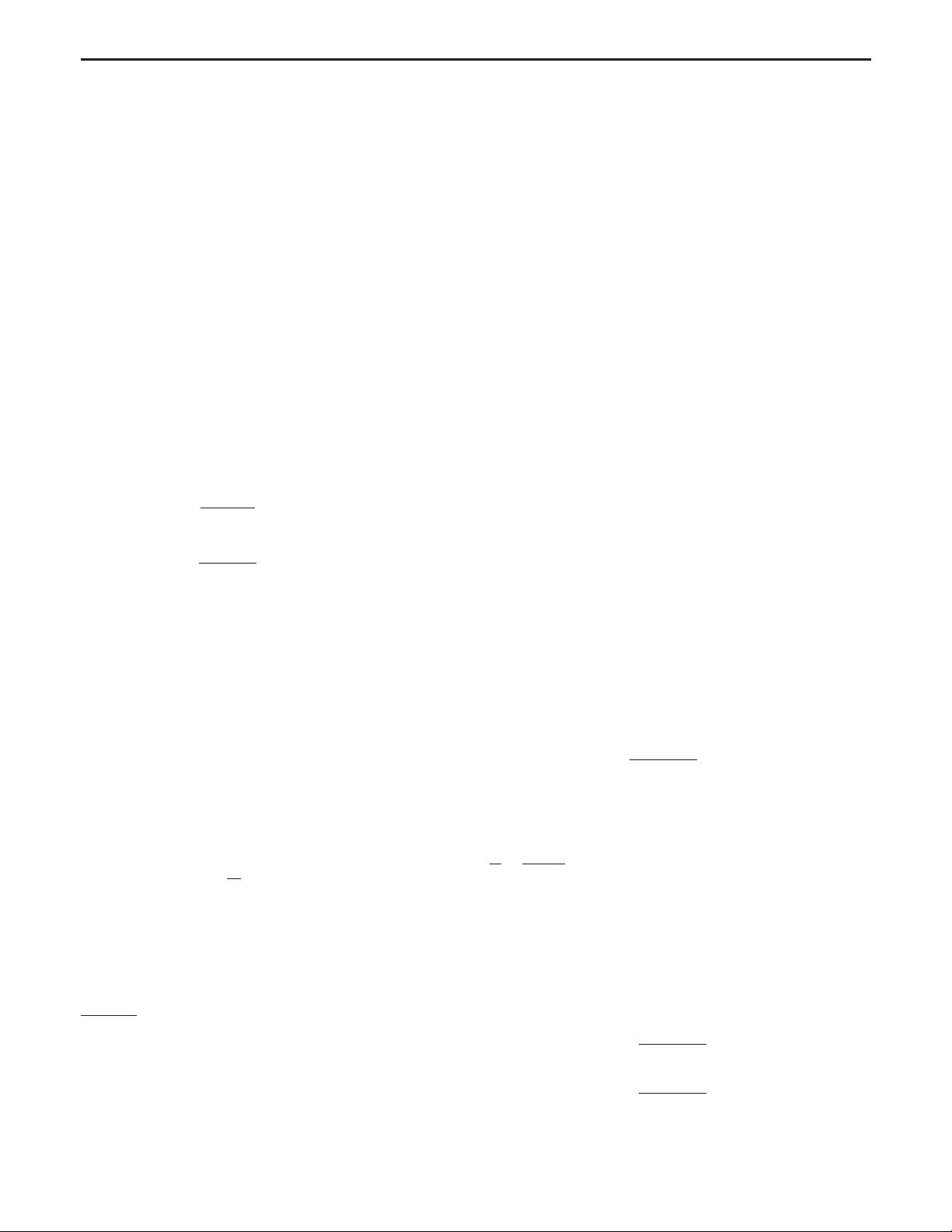
In the above, we have also used the relations

∂

f ¼ Φ

∂

f; ∂

f ¼ Φ

∂

f þ Φ

∂

f: ð18Þ

The lhs of Eq. (17) is positive; therefore the same should

hold for the rhs, too. Note that, for Λ > 0, Eq. (17) demands

that, at least at y → ∞, the coupling function fðΦÞ should

be negative for the scalar field to have a real first derivative

there. Indeed, in [74], we presented two analytic solutions

of this theory where f<0 either far away from our brane

or in the entire bulk regime. In contrast, in the present case,

where Λ < 0, no such behavior is necessary; thus in order

to have a normal gravity over the entire five-dimensional

space-time, we assume that fðΦÞ is positive everywhere.

In order to have a physically acceptable behavior, a few

more properties should be assigned to the functions Φ ¼

ΦðyÞ and f ¼ f½ΦðyÞ. Both functions should, of course,

be real and finite in their whole domain and of class C

∞

.At

y → ∞, both functions should satisfy the following rela-

tions; otherwise the finiteness of the theory at infinity

cannot be ascertained,

lim

y→∞

½fðyÞ

¼ 0; ∀ n ≥ 1; ð19Þ

lim

y→∞

½ΦðyÞ

¼ 0 ; ∀ n ≥ 1: ð20Þ

These constraints guarantee that all components of the

energy-momentum tensor T

ðΦÞM

will be real and finite

everywhere, and, in addition, localized close to our brane.

Then, demanding also the finiteness and the vanishing of

the rhs of Eq. (17) due to the constraint (20), we conclude

that the coupling function fðyÞ should, at infinity, decrease

faster

than e

−2ky

, i.e., fðyÞ should be of the form

fðyÞ¼f

gðyÞ

;



> 0

gðy → ∞Þ < −2ky



: ð21Þ

Consequently, upon integrating Eq. (17), the following

expression is obtained for the scalar field:

ΦðyÞ¼

ﬃﬃﬃﬃﬃ

dye

gðyÞ

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

2ky

− g

− kg

; ð22Þ

where, for convenience, we have also set Λ ¼ −

.In

order to proceed further, we need to determine the exact

form of the function gðyÞ. As we are interested in deriving

analytical solutions for both functions fðyÞ and ΦðyÞ, the

function gðyÞ should have a specific form in order to result

in a solvable integral on the rhs of Eq. (22). Therefore, we

make the following two choices:

gðyÞ¼−λky; λ ∈ ð2; þ∞Þ; ð23Þ

gðyÞ¼−μ

λy

;



λ ∈ ð0; þ∞Þ

μ ∈ ℜnf0g



: ð24Þ

The aforementioned expressions for gðyÞ ensure that

both fðyÞ and ΦðyÞ have the desired properties outlined

above and, in addition, lead to analytical solutions. In the

following sections, these two different cases are studied

separately.

III. THE SIMPLE EXPONENTIAL CASE

We start with the simple exponential case (23), and

derive first the form of the scalar field and its potential in

the bulk. We then study their main characteristics in terms

of the free parameters of the model, and finally address the

effect of the junction conditions and the form of the

effective theory on the brane.

A. The bulk solution

In this case, we have fðyÞ¼f

−λky

, with f

> 0 and

λ > 2. Then, from Eq. (17), we obtain

ðyÞ¼fðyÞð

2ky

− λ

þ λk

Þ ≥ 0: ð25Þ

For a nonzero and positive fðyÞ, the above inequality

demands that the combination inside the brackets should be

positive. As this is an increasing function of y, it suffices to

demand that this holds at the location of the brane, at y ¼ 0.

Then, we obtain the following constraint on the parameters

of the theory:

λðλ − 1Þk

> 1: ð26Þ

The function Φ

ðyÞ could, in principle, be 0 at the point

where ΦðyÞ has an extremum. However, from Eq. (25),we

may easily see that this may happen only at y

lnð

λðλ−1Þk

Þ, which, upon using Eq. (26), turns out to

be negative. Therefore, the scalar field does not have any

extremum in the whole domain 0 ≤ y<∞, which in turn

means that ΦðyÞ is a one-to-one function in the same

region. The Z

symmetry of the extra dimension ensures

that this result holds in the region y<0 as well. We note

this property for later use.

Equation (17) can be rewritten as

ðΦ

¼ f

λðλ − 1Þk



λðλ − 1Þk

2ky

− 1



−λky

¼ f

λðλ − 1Þk



λðλ − 1Þk



λ=2

ðw − 1Þw

−λ=2

; ð27Þ

Note that allowing the coupling function to vary exactly as

−2ky

, i.e., fðyÞ¼f

−2ky

, would lead to a finite, constant value

of Φ

at infinity, namely, Φ

∞

¼ −f

Λ > 0. This would amount

to having a diverging field at the boundary of spacetime but

nevertheless finite, constant values for the components of the

energy-momentum tensor. We come back to this point later.

NEW BLACK-STRING SOLUTIONS FOR AN ANTI–DE SITTER … PHYS. REV. D 99, 124040 (2019)

124040-5

剩余20页未读，继续阅读

weixin_38586279

粉丝: 2
资源: 949

五维标量张量重力中的反de Sitter弦状黑洞解

退化高阶标量张量理论中隐身黑洞的扰动

标量-张量重力中标度解的搜索

带电的标量张量孤子和黑洞，具有（近似）Anti-de Sitter渐近性

标量张量理论中的稳定虫洞

标量张量模型中具有指数势的慢滚充气

标量张量引力理论中的Palatini框架

从标量张量理论和f（T）重力中的不均匀状态方程重建

太阳系实验会限制标量-张量重力吗？

引力的扩展标量张量理论

惯性和标量张量宇宙学对无菌中微子的影响

最新资源