JAVA实现哈夫曼树：最小带权路径详解

java实现哈夫曼树
哈夫曼树的构造
java
java哈夫曼编码
5星 · 超过95%的资源 3 下载量 19 浏览量 更新于2024-09-01 1 收藏 121KB PDF 举报
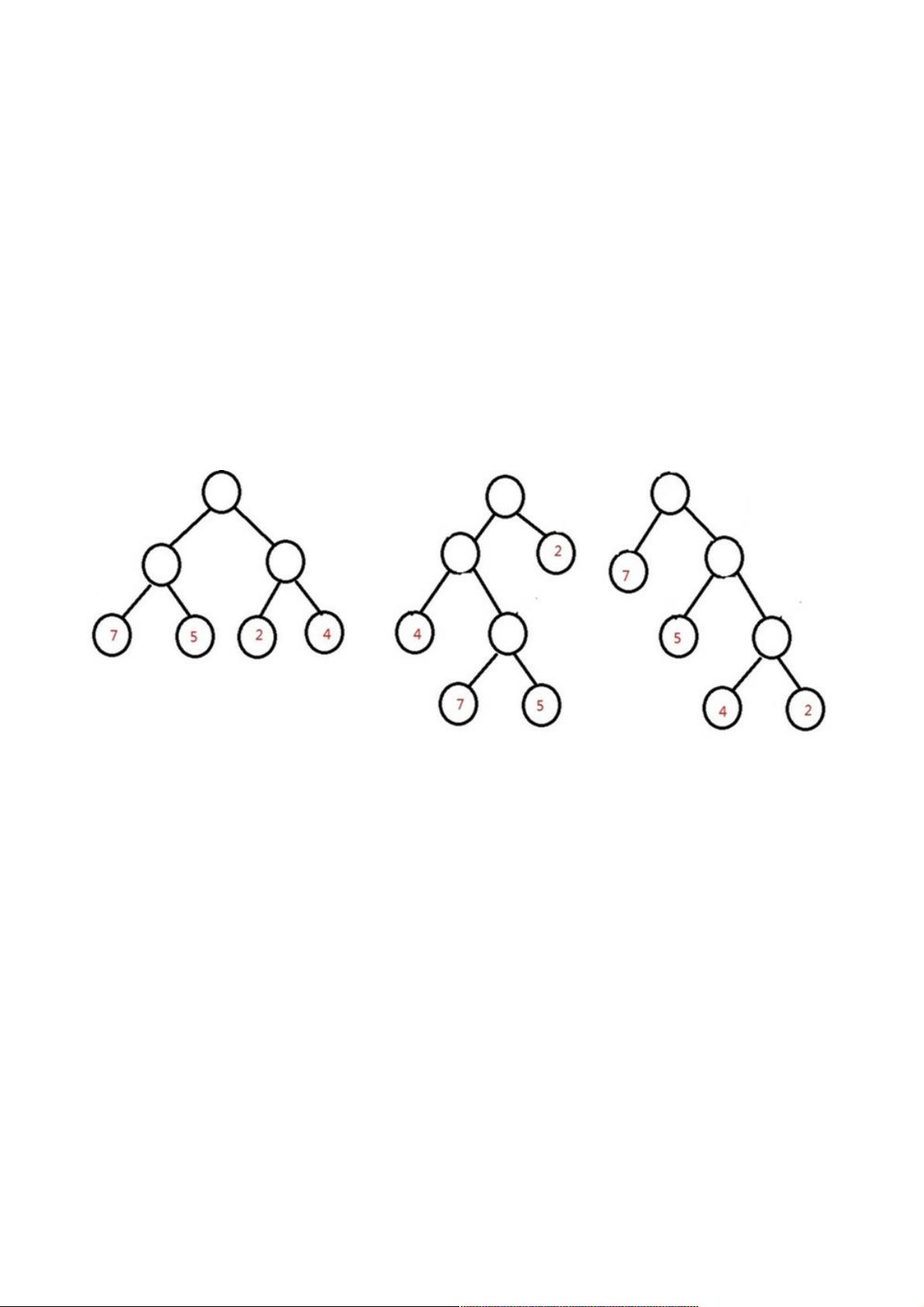
"图文详解JAVA实现哈夫曼树" 哈夫曼树是一种特殊的二叉树，也被称为最优二叉树或最小带权路径长度树。它主要用于数据压缩和哈夫曼编码，是由美国计算机科学家大卫·艾伦·哈夫曼(David A. Huffman)提出的。哈夫曼树的主要特点是其具有最小的带权路径长度，即树中所有叶子节点的权值乘以其到根节点的路径长度之和最小。 在构建哈夫曼树的过程中，通常遵循以下步骤： 1. **统计权值**：首先，我们需要知道每个元素（如字符）的频率或权值。例如，在给定的字符串"aaaaaaaaaabbbbbaaaaaccccccccddddddfff"中，字符'a'出现了15次，'b'出现了5次，'c'出现了8次，'d'出现了6次，'f'出现了3次。 2. **创建初始最小堆**：将这些权值视为单独的节点，放入一个优先队列（最小堆）中。每个节点都是一个带有权值的叶节点。 3. **合并最小节点**：每次从队列中取出两个权值最小的节点，将它们合并成一个新的内部节点，该节点的权值为这两个子节点的权值之和。新节点的两个子节点分别对应原来的两个小节点，然后将新节点放回队列。 4. **重复合并过程**：持续执行此操作，直到队列中只剩下一个节点，这个节点就是哈夫曼树的根节点。 5. **构建哈夫曼树**：随着合并过程，我们可以构建出完整的哈夫曼树。在上面的例子中，最终的哈夫曼树将包括节点'dfb14'、'a15'和'c8'。其中，'fb8'是合并'b5'和'f3'得到的，'dfb14'是合并'dfb8'和'a15'得到的，而整个树的根节点是'dfb14'。 哈夫曼树在Java中实现，通常会用到数据结构如`PriorityQueue`（优先队列）来辅助构建。通过不断地从队列中取出权值最小的节点并合并，直到队列为空，即可得到哈夫曼树。在Java中，可以使用`Comparator`来比较节点的权值，确保每次取出的都是最小的。 哈夫曼树的构建不仅限于字符频率统计，还可以用于其他场景，如网络传输优化、数据存储等，因为它的核心思想是优化资源分配，使得整体效率最大化。在实际应用中，哈夫曼编码常用于数据压缩，通过对数据进行编码，减少存储空间和传输时间。 总结起来，哈夫曼树是一种基于最小带权路径长度构建的二叉树，它在Java中可以通过优先队列等数据结构实现。掌握哈夫曼树的构建和应用对于理解和优化数据处理算法至关重要。

java基于链表实现树结构(算法源码)

2010-01-15 上传
/* * 基于链表实现树结构 */ package dsa; public class TreeLinkedList implements Tree { private Object element;//树根节点 private TreeLinkedList parent, firstChild, nextSibling;//父亲、长子及最大的弟弟 //（单节点树）构造方法 public TreeLinkedList() { this(null, null, null, null); } //构造方法 public TreeLinkedList(Object e, TreeLinkedList p, TreeLinkedList c, TreeLinkedList s) { element = e; parent = p; firstChild = c; nextSibling = s; } /*---------- Tree接口中各方法的实现 ----------*/ //返回当前节点中存放的对象 public Object getElem() { return element; } //将对象obj存入当前节点，并返回此前的内容 public Object setElem(Object obj) { Object bak = element; element = obj; return bak; } //返回当前节点的父节点；对于根节点，返回null public TreeLinkedList getParent() { return parent; } //返回当前节点的长子；若没有孩子，则返回null public TreeLinkedList getFirstChild() { return firstChild; } //返回当前节点的最大弟弟；若没有弟弟，则返回null public TreeLinkedList getNextSibling() { return nextSibling; } //返回当前节点后代元素的数目，即以当前节点为根的子树的规模 public int getSize() { int size = 1;//当前节点也是自己的后代 TreeLinkedList subtree = firstChild;//从长子开始 while (null != subtree) {//依次 size += subtree.getSize();//累加 subtree = subtree.getNextSibling();//所有孩子的后代数目 } return size;//即可得到当前节点的后代总数 } //返回当前节点的高度 public int getHeight() { int height = -1; TreeLinkedList subtree = firstChild;//从长子开始 while (null != subtree) {//依次 height = Math.max(height, subtree.getHeight());//在所有孩子中取最大高度 subtree = subtree.getNextSibling(); } return height+1;//即可得到当前节点的高度 } //返回当前节点的深度 public int getDepth() { int depth = 0; TreeLinkedList p = parent;//从父亲开始 while (null != p) {//依次 depth++; p = p.getParent();//访问各个真祖先 } return depth;//真祖先的数目，即为当前节点的深度 } }

哈夫曼编码压缩程序（Java）

2016-12-18 上传
用面向对象的程序设计思想自己动手写压缩软件，采用了优先队列这一很好的数据结构实现的贪心算法构造Huffman树，能打印Huffman树，显示编码表，压缩文件和解压缩文件，采用UTF-8字符集，支持中文文件

哈夫曼树实现

2016-06-04 上传
实现哈夫曼树

java实现哈夫曼树.docx

2023-10-18 上传
在上述Java代码中，我们看到了如何实现哈夫曼树（Huffman Tree）的数据结构，以及利用该数据结构进行文本的编码和解码。哈夫曼树是一种特殊的二叉树，它的每个叶子节点代表一个字符，并且频率越高的字符，其对应的...

Java实现哈夫曼树存储空间管理：数据结构详解

点击了解资源详情
在本篇关于Java版数据结构的文章中，主要探讨的是如何为哈夫曼树分配存储空间。哈夫曼树，又称最优二叉树或最小带权路径长度树，是一种特殊的二叉树，用于解决编码问题，尤其在数据压缩中非常实用。它通过对输入数据...

Java实现哈夫曼树：构建最优二叉树的详解及代码

点击了解资源详情
尽管这段代码示例简化了部分细节，如排序和完整的树结构构建，但它展示了如何用Java实现哈夫曼算法的基本骨架。通过学习这个实现，开发者可以更好地理解哈夫曼树的构造过程，并在实际项目中应用这种算法，例如在文本...

Java实现哈夫曼树数据结构

点击了解资源详情
"java哈夫曼树数据结构.docx" 在计算机科学中，哈夫曼树（Huffman Tree），也称为最优二叉树，是一种特殊的二叉树，它用于数据编码和压缩，特别是在文本压缩领域中广泛应用。哈夫曼树的核心特性是其能够使树的带权...

java实现哈夫曼树

2024-06-15 上传
Java中实现哈夫曼树（Huffman Tree），也称为最优二叉树或霍夫曼编码树，通常用于数据压缩算法。这里是一个简单的步骤和代码示例： 1. **构建频率表**：首先，收集并统计每个字符在输入序列中的出现频率。 2. **...

java 实现哈夫曼树

2023-04-17 上传
Java 实现哈夫曼树，可以通过先构建哈夫曼树，再进行哈夫曼编码。哈夫曼树的构建可以使用最小堆来实现。首先，将每个字符作为叶子节点，并将它们的权值作为键值存储在最小堆中。然后，反复取出最小的两个节点，并将...

Java 实现哈夫曼树

2023-04-17 上传
好的，我会尽力回答你关于Java实现哈夫曼树的问题。在Java中实现哈夫曼树，可以通过使用优先队列（PriorityQueue）来实现。首先，需要定义一个节点类来表示哈夫曼树的每个节点，包括权值、左子树和右子树。然后，...
weixin_38606656
  • 粉丝: 4
  • 资源: 896
上传资源 快速赚钱

最新资源