CPT107离散数学复习重点:数据类型与证明方法
需积分: 0 44 浏览量
更新于2024-06-27
4
收藏 2.64MB DOCX 举报
"这份笔记是针对XJTLU大学CPT107课程——离散数学的期末复习资料,包含了全面的知识梳理和一些个人复习经验。笔记详细讨论了基本数据类型、证明方法、集合论和关系等方面的内容,旨在帮助后续学习者备考。同时,笔记作者提醒考生注意考试时间管理,并提供了配套例题以供练习。"
详细说明:
离散数学是计算机科学中的基础学科,它研究的是离散而非连续的对象。这份笔记首先介绍了最基本的数据类型:
1. 自然数:包括所有非负整数,通常用N表示,是计算的基础。
2. 整数:包含正整数、零和负整数,表示为Z。
3. 有理数:可以表示为两个整数比例的数,包括分数和小数,记作Q。
4. 实数:包括有理数和无理数,构成实数集R,是数学分析的核心。
5. 素数:只能被1和自身整除的正整数,是数论研究的重要对象。
接下来,笔记讲解了证明技巧:
2.1 找反例:通过找到一个反例来否定一个命题的有效性。
2.2 反证法:假设命题的否定为真,然后推导出矛盾,从而证明原命题为真。
在集合论部分:
3.1 符号:如大括号{}用于表示集合,逗号分隔元素。
3.2 重要集合:如自然数集N,整数集Z,有理数集Q,实数集R。
3.3 子集:一个集合的元素全部属于另一个集合,前者称为后者的子集。
3.4 等同:两个集合元素完全相同则它们等同。
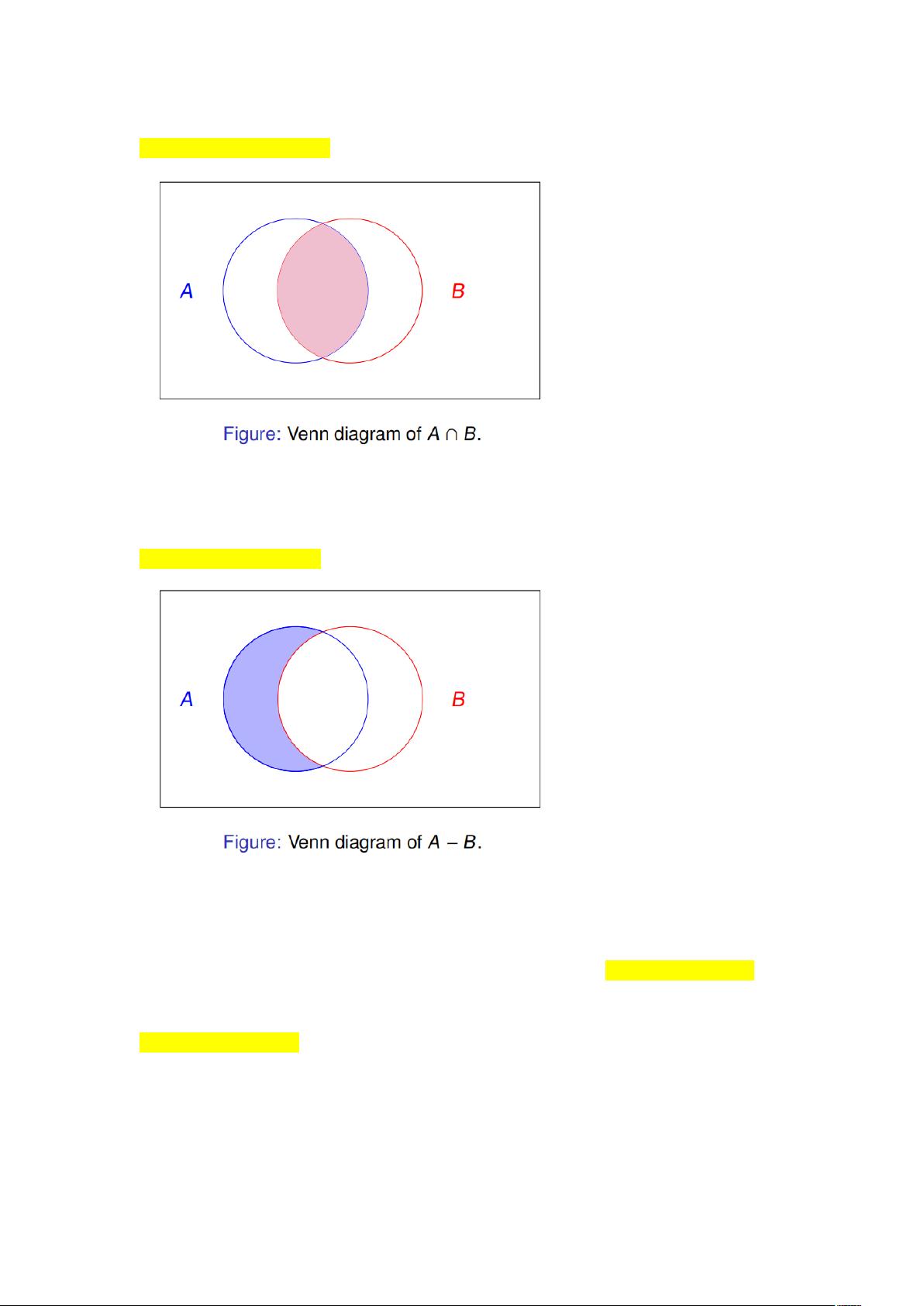
3.5 集合操作:包括并集、交集、相对补集、补集和对称差。
3.6 集合运算定律:如交换律、结合律、分配律等。
3.7 Power Set:一个集合的所有子集构成的集合,称为幂集。
3.8 基数:表示集合中元素的个数。
3.9 笛卡尔积:两个集合的笛卡尔积是所有可能的有序对组成的集合。
关系部分:
4.1 二元关系:定义在两个集合上的关系。
4.1.2 表示方法:可以用矩阵、图或列表来表示。
4.1.3 一元关系:只涉及一个集合的特殊二元关系。
4.1.4 中缀表示法:如xRy表示x与y之间存在关系R。
4.1.5 二元关系性质:如自反性、对称性和传递性。
4.2 闭包:通过特定运算得到的关系,如自反闭包、对称闭包和传递闭包。
4.3 等价关系:满足自反性、对称性和传递性的二元关系。
4.4 集合的划分:将集合分割成不相交且覆盖整个集合的子集。
4.4.1 连接分区和等价关系:等价关系下的等价类形成集合的划分。
4.4.2 偏序:满足自反性和反对称性的二元关系,但不一定是传递的。
4.4.3 可比较/不可比较:在偏序集中,两个元素要么是可比较的(即其中一个在另一个之上),要么是不可比较的。
这些内容构成了离散数学的基础,对于理解和应用计算机科学中的算法和理论至关重要。通过深入学习和理解这些概念,学生将能更好地掌握离散结构,并在编程、数据结构、算法设计等领域中运用自如。
607 浏览量
911 浏览量
2021-10-12 上传
2021-03-11 上传
169 浏览量
Scabbards_
- 粉丝: 1266
- 资源: 2
最新资源
- 计算机等级考试试题计算机等级考试试题
- CSS 中文手册详解
- Android A Programmer's Guide
- jsp网络程序设计课件
- loadrunner中文帮助文档
- Java Reflection in Action
- 软件开发常用英语词汇
- 实例讲解如何排除路由器常见故障
- Linux_C函数库参考手册.doc
- The+Accredited+Symbian+Developer+Primer.pdf
- Expert F# Functional Programming
- Toad 使用快速入门.doc
- ArcGIS Engine的开发与部署
- qtp与td连接方法及常见问题解决方法
- Event-Handling
- 软件工程思想 (视野独特,构思新颖,内容风趣,不落窠臼,令人耳目一新)