MATLAB实现图像傅里叶变换:揭示频率组成
需积分: 22 3 浏览量
更新于2024-07-19
2
收藏 10.26MB PPT 举报
本文档主要介绍了如何使用MATLAB进行图像的傅里叶变换,这是一种在数字信号处理和图像分析中常用的技术。傅里叶变换是将一个时域信号分解为一系列不同频率分量的过程,有助于揭示信号的频域特性,对于理解复杂信号如图像的频谱构成至关重要。
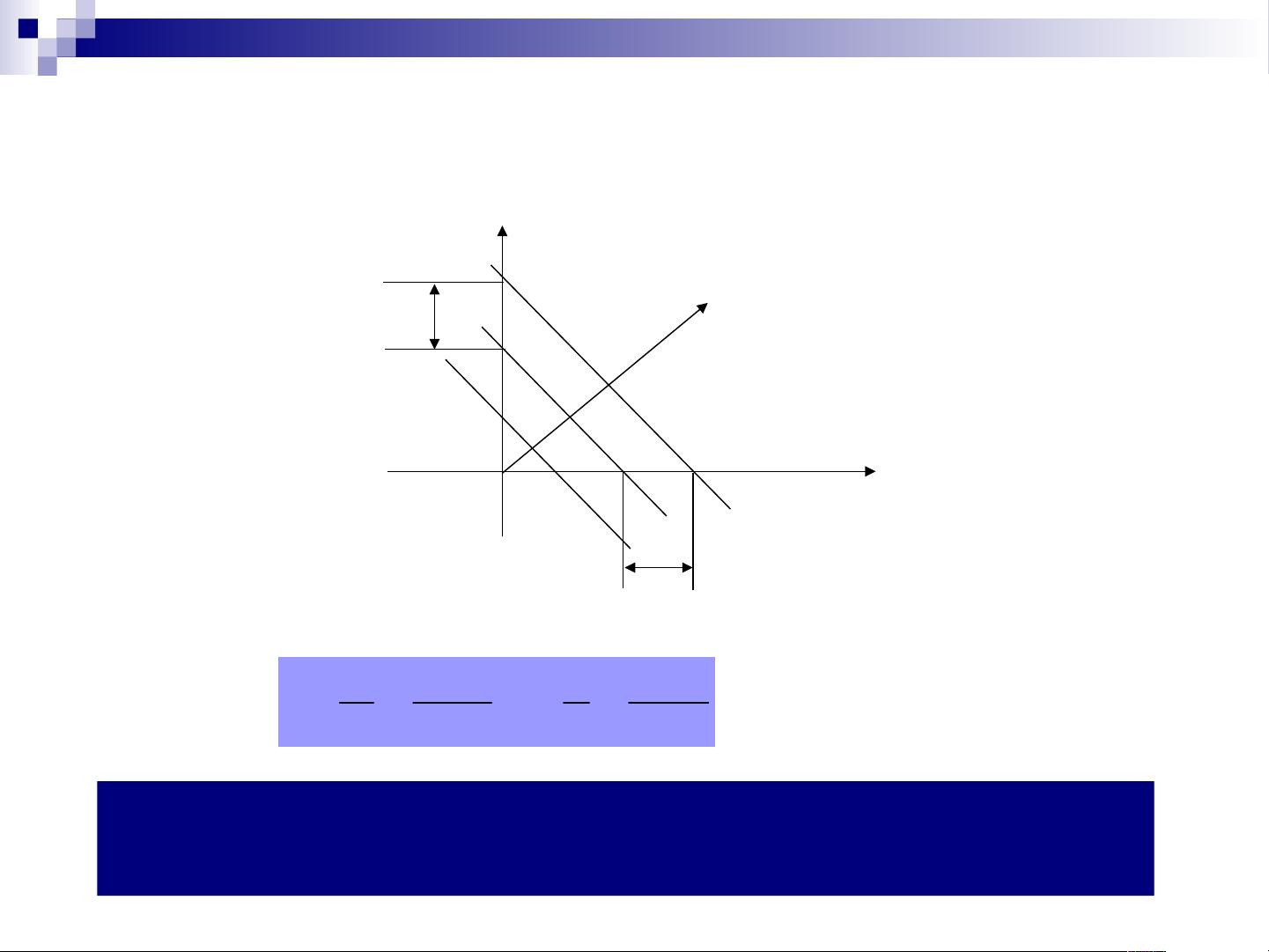
首先,文章区分了一维连续傅里叶变换(Continuous Fourier Transform, CFT)和其反变换,以及离散傅里叶变换(Discrete Fourier Transform, DFT)和对应的反变换。CFT适用于连续函数,而DFT则针对离散函数,如图像像素。DFT的特点在于通过欧拉公式将离散函数转换为包含正弦和余弦乘积的形式,其中不同的u值对应不同的频率成分。
傅里叶变换的作用体现在以下几个方面:
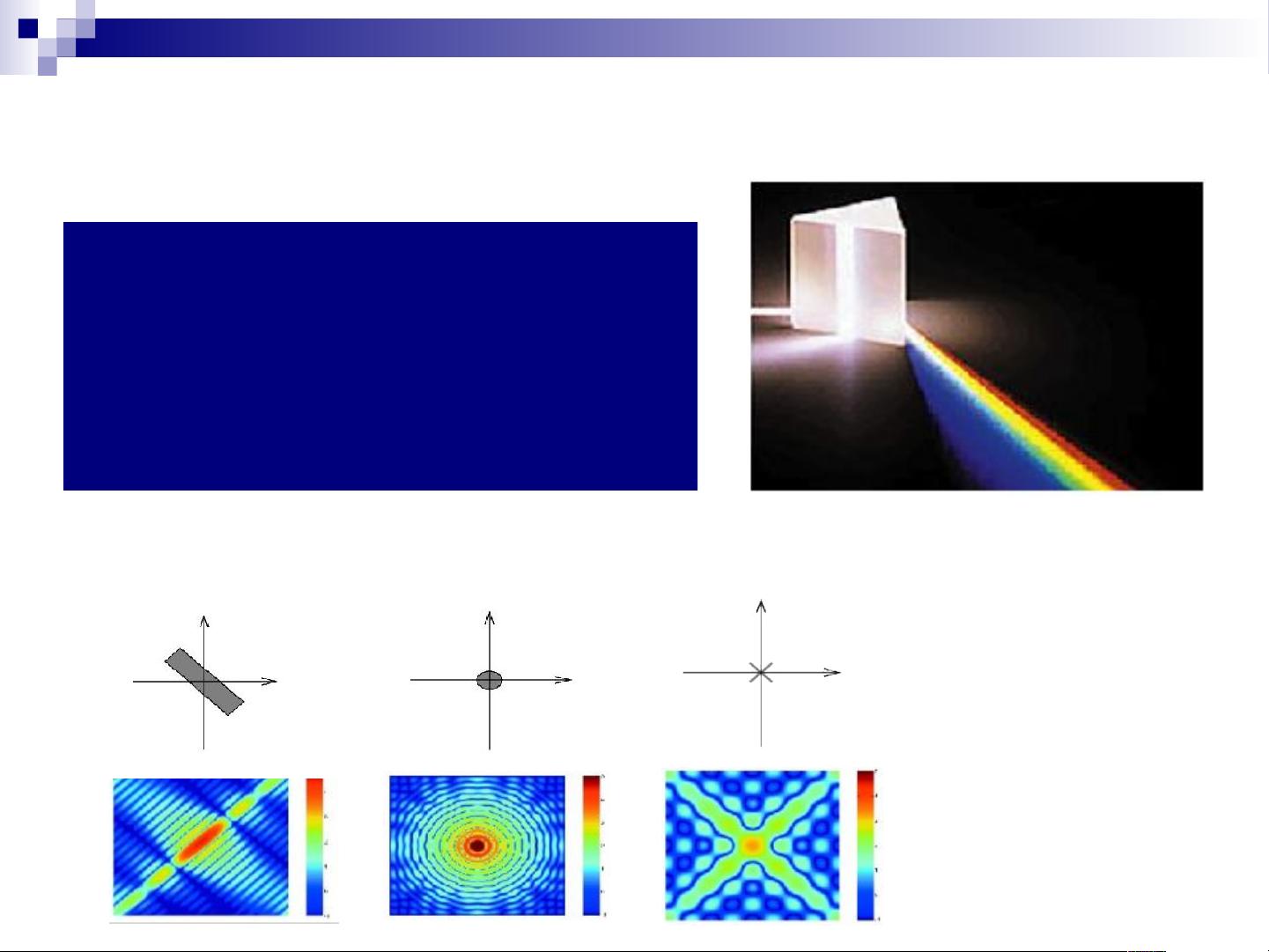
1. **频域分析**:它将信号分解为不同频率的部分,类似于光学中的分色棱镜,使我们能观察到信号在不同频率上的分布,这对于噪声滤波、信号特征提取和图像压缩等应用非常重要。
2. **频率成分**:信号被划分为直流分量(频率为零的恒定信号)和交流分量(非零频率的周期性信号),这有助于识别信号中的静态和动态部分。
3. **频率与速度关联**:图像中的高频部分通常对应于噪声、边缘和快速变化区域,而低频部分则表示背景区域和缓慢变化部分。
对于二维图像,文档介绍了二维离散傅里叶变换(2D DFT),这是对图像每个像素进行一维DFT后再对所有行和列的结果进行组合。2D DFT提供了关于图像整体频率特性更为全面的信息,对于图像处理中的滤波、增强和特征检测任务尤为关键。
在实际操作中,MATLAB提供了内置函数如`fft2`和`ifft2`来计算和逆变换2D DFT,以及处理图像的频域分析。通过这个工具,用户可以方便地探索和理解图像在频域的结构,进而优化图像处理算法和提高分析精度。
总结来说,该文档详细阐述了MATLAB中图像傅里叶变换的基础理论和实际应用,是深入理解并运用这一技术的重要参考资料。
点击了解资源详情
点击了解资源详情
319 浏览量
386 浏览量
312 浏览量
2024-10-13 上传
2024-11-16 上传
点击了解资源详情
开心就哈哈
- 粉丝: 23
最新资源
- Java图片爬虫程序深入解析:连接数据库实现高效下载
- Panasonic SDFormatter:专业SD卡格式化解决方案
- 官方发布:单片机下载器驱动程序安装与使用指南
- 深入理解Cloud Post - 构建Node.js应用与安全实践
- Android网络检测技术示例:检测不可用WiFi连接
- MSP430F149烧录软件使用与USB-BSL驱动下载指南
- 揭秘网站安全编程:防止xss漏洞的实战技巧
- Java推箱子游戏开发教程及实践
- 使用PHP将Markdown转换为HTML的简易教程
- J2ME推箱子游戏开发:课程设计与移动运行指南
- 邮政编码识别:利用OPENCV技术进行倾斜矫正与字符分隔
- 揭秘无刷电机霍尔传感器与绕组位置对应关系
- OMics患者报告生成与R软件包安装指南
- 使用xmlbeans-2.4.0快速生成JAVA代码的方法
- suit.less:简化 LESS 编写,兼容 Suitcss 样式
- C#连接Access创建密码管理器简易操作指南