有源滤波器的低通与高通相位响应详解

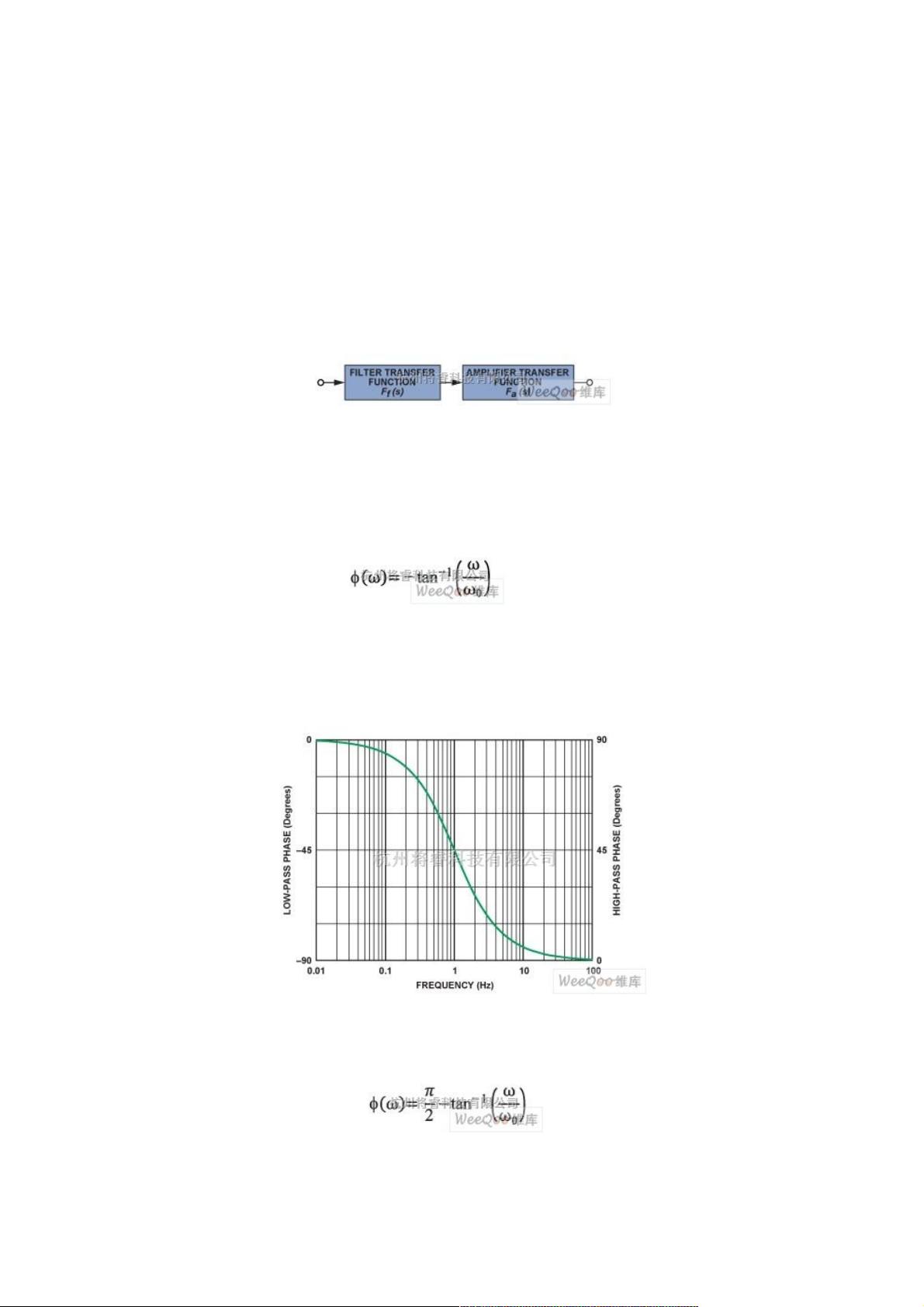
在单片机与DSP技术中，有源滤波器的设计不仅关注其幅度响应，因为相位响应在许多应用场景如延时仿真、级联滤波器电路和过程控制环路中扮演着关键角色。本文主要探讨的是低通和高通滤波器的相位响应特性。 低通滤波器，其传递函数的相位响应可以用单极点滤波器的公式表示，即相移与角频率ω的关系，具体为 ϕ = -atan(ω/ω0)，其中ω0是滤波器的中心频率，决定了相移的变化趋势。在图2（左轴）中，我们可以看到随着频率偏离中心频率，相位从0°逐渐增加到最大值-45°，当频率等于中心频率时，相移为-90°或-π/2弧度，这是低通滤波器典型的行为特征。 高通滤波器的相位响应则是相反的过程。其相移公式为 ϕ = atan(ω/ω0)，此时相移从0°开始，随着频率的升高逐渐增加，达到45°。图2（右轴）展示了这一特性，高通滤波器的中心频率相移为+45°，这表示在高于中心频率的区域，相位增益增大。 理解这些基本的相位响应有助于设计者在选择滤波器时，根据具体的应用需求来调整通带内的相位变化，例如在过程控制系统中，稳定的相位响应对于避免振荡和失真至关重要。后续的文章将会进一步探讨带通滤波器、陷波(带阻)滤波器、全通滤波器以及滤波器对脉冲和阶跃输入的响应，这些都是构建高效信号处理系统的重要组成部分。掌握这些基本原理对于在单片机和DSP中实现精确的信号滤波至关重要。