中国人口预测:数学模型与Leslie矩阵法
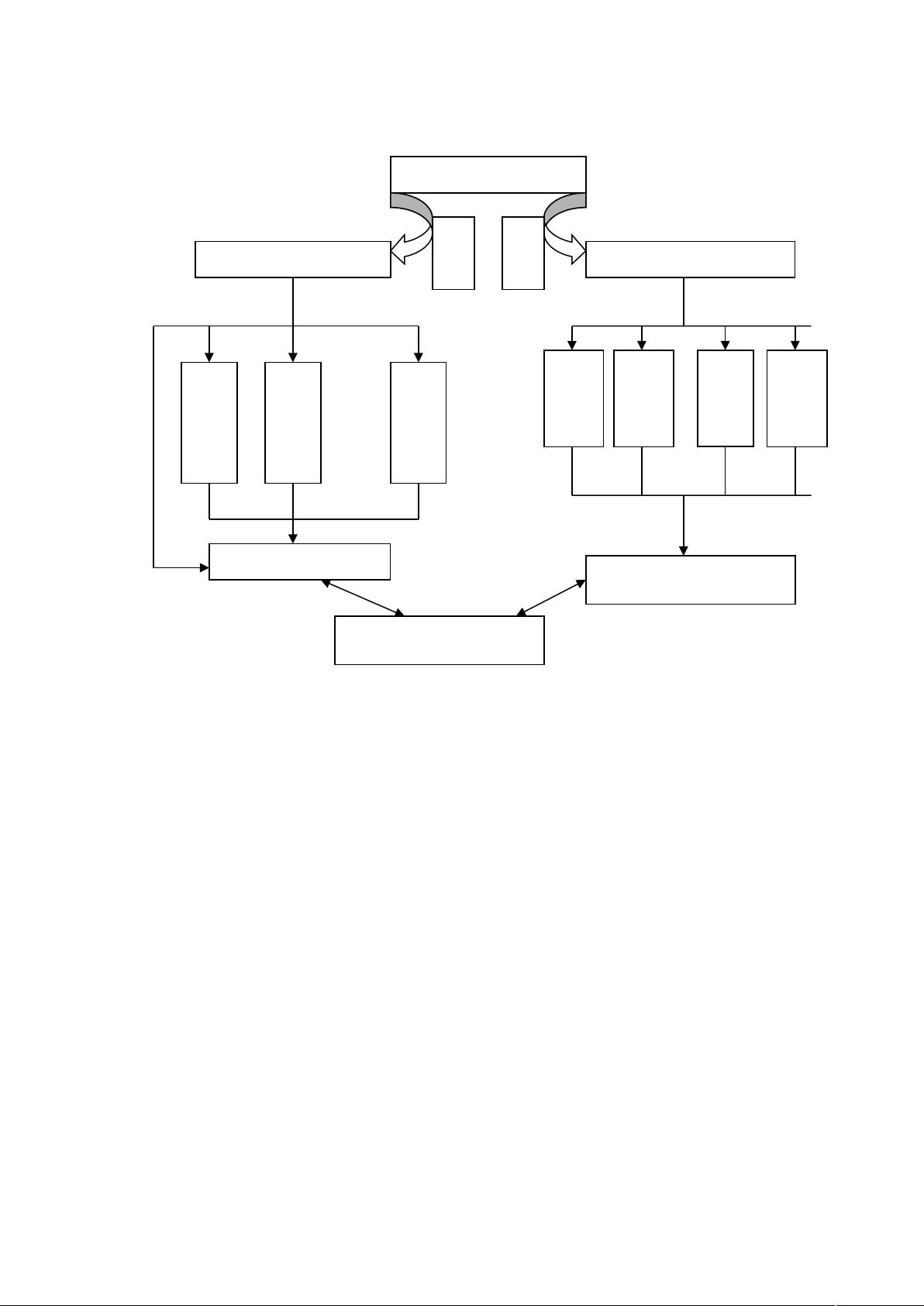
本文探讨了人口预测模型的构建与应用,包括一次线性回归模型、灰色序列预测模型、逻辑斯蒂模型以及Leslie人口模型。通过加权组合模型,结合不同模型的预测误差,对人口数量进行综合预测,并分析了生育率、死亡率、年龄结构等因素对人口增长的影响。
在人口预测领域,数学模型起着至关重要的作用。一次线性回归模型是最基础的预测工具,它假设人口增长与时间呈线性关系。然而,由于人口变化的复杂性,一次线性模型可能无法完全捕捉到人口动态。因此,文中引入了灰色序列预测模型,这是一种适用于小样本、非完整信息数据的预测方法,它通过挖掘数据内在的灰色关联性来预测未来趋势。
逻辑斯蒂模型则是基于人口增长率饱和的假设,考虑了环境承载力的限制,通常用于人口饱和状态的预测。但是,它忽略了人口结构和性别比例等具体因素。
为克服单一模型的局限性,文章采用加权法构建了熵权组合模型,通过分配不同的权重给各个模型,使得预测误差最小化。例如,对于2006年至2010年的人口预测,加权系数分别为0.24282、0.34055和0.41663,这种组合方法可以提高预测的准确性和稳定性。
Leslie人口模型是一种更全面的人口预测模型,它考虑了生育率和死亡率的年龄依赖性,以及性别比例对人口结构的影响。通过分别以1年和5年为分组长度,模型能够预测短期和长期的人口变化。例如,预测显示2006年至2012年间,人口呈现稳定增长;而在更长远的时间段,如2016年至2050年,人口总数呈现出波动上升的态势。
为了验证模型的有效性,文中还提供了实际历史人口数据作为对比。例如,1993年至2005年的总人口数据,以及使用Matlab软件处理后的原始数据序列和新数列,这些数据有助于评估模型的预测精度。
人口预测模型的构建需要综合考虑多种因素,并且通过比较不同模型的预测结果,选择最佳的预测策略。这不仅对于政策制定者制定人口政策至关重要,也为社会经济规划提供科学依据。通过对历史数据的深入分析和模型的不断优化,我们可以更准确地预测未来人口发展趋势,从而更好地应对由此带来的挑战。
235 浏览量
1975 浏览量
2429 浏览量
179 浏览量
637 浏览量
11180 浏览量
小蛮腰的魅力
- 粉丝: 0
- 资源: 1
最新资源
- 英语常用3500词音频+PDF文件(含音频).zip
- 老板计时器
- Honey Boo Boo的算法和功能分解
- ember-addon-config
- 1.8wUA库.zip
- reading-notes:在这里您可以找到我的阅读资料库,主要用于总结我在编程方面的学习历程,希望您能找到一些有用的信息<3
- 视频播放可弹出弹幕,关闭弹幕
- simple-spawner:生成一个命令并将输出通过管道返回到 std{in,out,err}
- CSS_Assignment_2
- 使用注释将JDBC结果集映射到对象
- curious-blindas-api:CuriousCat克隆
- PRO-C21-BULLETS-AND-WALLS
- ff35mm:Flickr 的全画幅 (35mm) 焦距
- C#解析HL7消息的库
- 将Java System.out定向到文件和控制台的快速简便方法
- 库索逻辑-葡萄牙语