Java编程求解线性方程组的步骤与方法

"本文档介绍如何使用Java编程语言求解线性方程组，通过示例解释了解决步骤和矩阵变换方法，包括交换行、行乘以常数和行替换等操作，最终达到标准型增广矩阵，并提供了交换行的Java代码片段。" 线性方程组的求解是数学中的基础问题，在计算机科学和工程领域有广泛应用。本文档主要讨论如何用Java来实现这一过程。线性方程组的解法通常涉及高斯消元法或高斯-约旦消元法，这两种方法都依赖于矩阵的行变换来逐步将增广矩阵转化为阶梯形或最简行阶梯形。 首先，对于一个线性方程组，可以将其表示为增广矩阵，即在系数矩阵的基础上增加一列，包含方程的常数项。例如，给定的三维线性方程组可以通过创建一个3x4的矩阵来表示，其中最后一列是右侧常数项（RHS）。 在Java中，我们可以用二维数组来表示这个矩阵。处理线性方程组的关键在于通过合法的矩阵操作将其转化为标准型增广矩阵，即主对角线上的元素为1，其余非对角线元素为0，而最后一列保留原方程的常数项。这三种基本操作包括： 1. 行交换（操作A）：可以交换任意两行，以调整主对角线元素的位置。 2. 行乘以常数（操作B）：每行的所有元素可以乘以同一非零数，以调整主对角线元素为1或消除其他位置的非零元素。 3. 行替换（操作C）：可以用本行与其他行的倍数之和来代替本行，以消除非主对角线元素。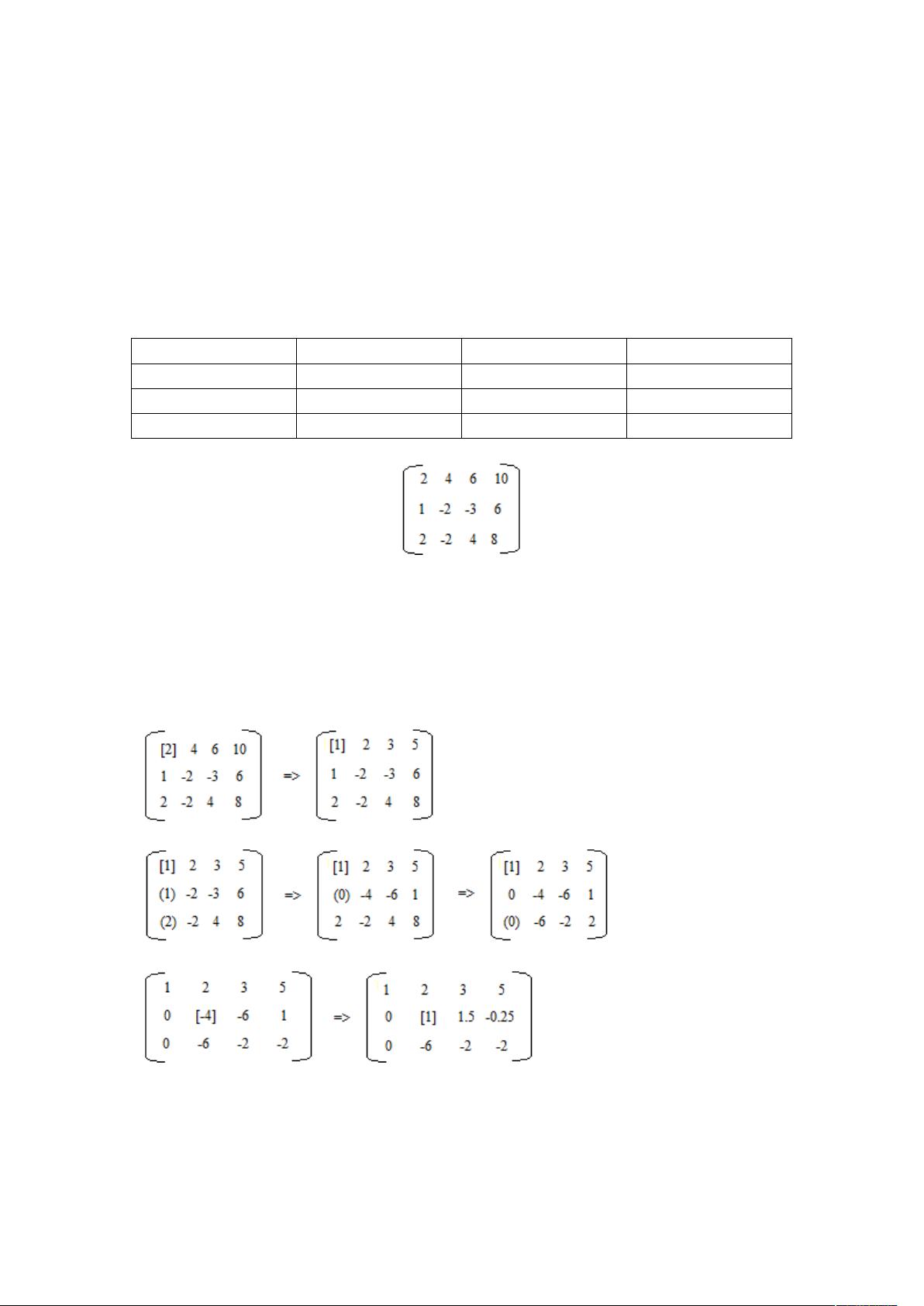 在给定的示例中，通过应用这些操作，逐步将初始的增广矩阵转换为标准型。例如，通过将第一行除以2，可以将[0][0]位置的元素变为1；然后通过行替换，依次消除其他行的首项，直至所有非主对角线元素为0。 在实际编程实现中，可以定义一个`swapRows`函数来执行行交换操作，如提供的Java代码片段所示。类似的，可以编写其他函数来执行行乘以常数和行替换操作。最后，通过这些矩阵操作，我们可以获得线性方程组的解，即每个变量的值。 对于更大的方程组，可以扩展这种方法，将矩阵操作封装到类或方法中，以便于处理更复杂的线性系统。在Java中，可以使用现有的库，如Apache Commons Math，它提供了矩阵操作的高级接口，简化了编程实现。 Java不仅可以用来求解简单的线性方程组，还可以处理大规模的线性系统，通过矩阵运算和适当的编程结构，可以实现高效且准确的求解过程。