多导弹分布式协同制导：固定与切换通信拓扑策略

69 浏览量更新于2024-07-15 收藏 1.63MB PDF 举报

本文探讨了具有固定和切换定向通信拓扑的多枚导弹分布式团体协作制导(Distributed Group Cooperative Guidance, DGCG)的问题。与传统的针对单个目标的协同制导不同，DGCG适用于同时或顺序攻击多个目标的场景。在这样的群体协作攻击中，导弹系统被划分为多个子组，每个子组负责攻击其特定的目标。导弹在同属于一个子组时需要同时到达目标，而不同的子组则按照预定的时间顺序进行协作。研究的焦点在于设计一种两步制导策略来实现这一目标。第一步采用基于局部信息的DGCG法则，导弹之间通过固定的定向通信网络进行协调，确保每个子组内的导弹形成协同动作。这一步涉及利用分布式控制理论，如网络优化和自适应控制算法，来处理多导弹系统中的复杂动态，并确保任务分配和路径规划的同步性。第二步是切换定向通信拓扑，当不同的子组开始行动时，通信结构可能会根据需要改变。这种灵活性允许导弹在不同的阶段使用不同的通信模式，比如星型、环形或网状通信，以优化信息传递效率和应对可能的干扰或故障。在切换过程中，导弹系统需要具备一定的自组织能力和容错能力，以确保即使在部分通信链路中断的情况下，攻击计划仍能顺利执行。该研究的重要贡献在于提出了一种适应性强且可扩展的框架，不仅能够应对多目标环境，还能适应通信条件的变化。它对军事应用具有实际价值，特别是在现代防空和反舰作战中，多枚导弹的协同操作可以显著提高打击精度和生存能力。非线性动力学分析和仿真结果展示了这种策略的有效性和鲁棒性，为未来更高级别的自主武器系统提供了理论基础。这篇研究论文深入挖掘了分布式导弹系统在复杂任务中的潜在优势，并通过理论建模和实证分析，为多枚导弹在动态环境中进行有效协作提供了实用的指导原则。它为军事技术的发展，尤其是智能武器系统的协同作战策略，开辟了新的研究方向。

2510 Q. Zhao et al.

defense system (i.e., T

). Without loss of generality,

suppose that the task assignment has been completed.

Subgroups M

and M

are expected to attack targets

and T

, respectively. To saturate the defenses and

increase the kill probability, T

should ﬁrst be destroyed

by subgroup M

, and then subgroup M

attacks T

Subgroups M

and M

work in coordination through

local inter-subgroup communications (i.e., information

exchange between different subgroups). In each sub-

group, multiple missiles synchronize the impact time

via local intra-subgroup communications (i.e., infor-

mation exchange within each subgroup). Thus, the

group cooperative attack can be achieved by the whole

multi-missile system.

Remark 1 In contrast to traditional cooperative guid-

ance, in which multiple missiles attack one single target

[12–25], the group cooperative guidance is employed

to intercept multiple targets. In addition, information is

exchanged not only within the same subgroup but also

between different subgroups. If there exist only one

subgroup and one target, then the group cooperative

guidance in the current paper becomes the traditional

one. Therefore, the group cooperative guidance prob-

lem can be treated as an extension of the traditional one

and has more generality.

The following assumptions are standard in studying

group behavior.

Assumption 1 ([30–34]) For all m

/∈ M

( p ∈

{1, 2,...,s}),



∀m

∈M

= 0.

Assumption 2 ([32,33]) {M

, M

,...,M

} is an

acyclic partition of the missile set M.

Remark 2 Assumption 1 means that the inter-subgroup

communication among different subgroups is either

positively or negatively weighted, as was pointed

out in [31]. The underlying physical meaning of the

inter-subgroup communications which are positively

and negatively weighted is explained as follows: On

the one hand, the positively weighted information

exchange can be viewed as the cooperative effects

among multiple subgroups. On the other hand, the neg-

atively weighted information exchange can be func-

tioned as the asynchronous effects among multiple

subgroups. The cooperative effects and asynchronous

effects ensure that all the subgroups work as a whole

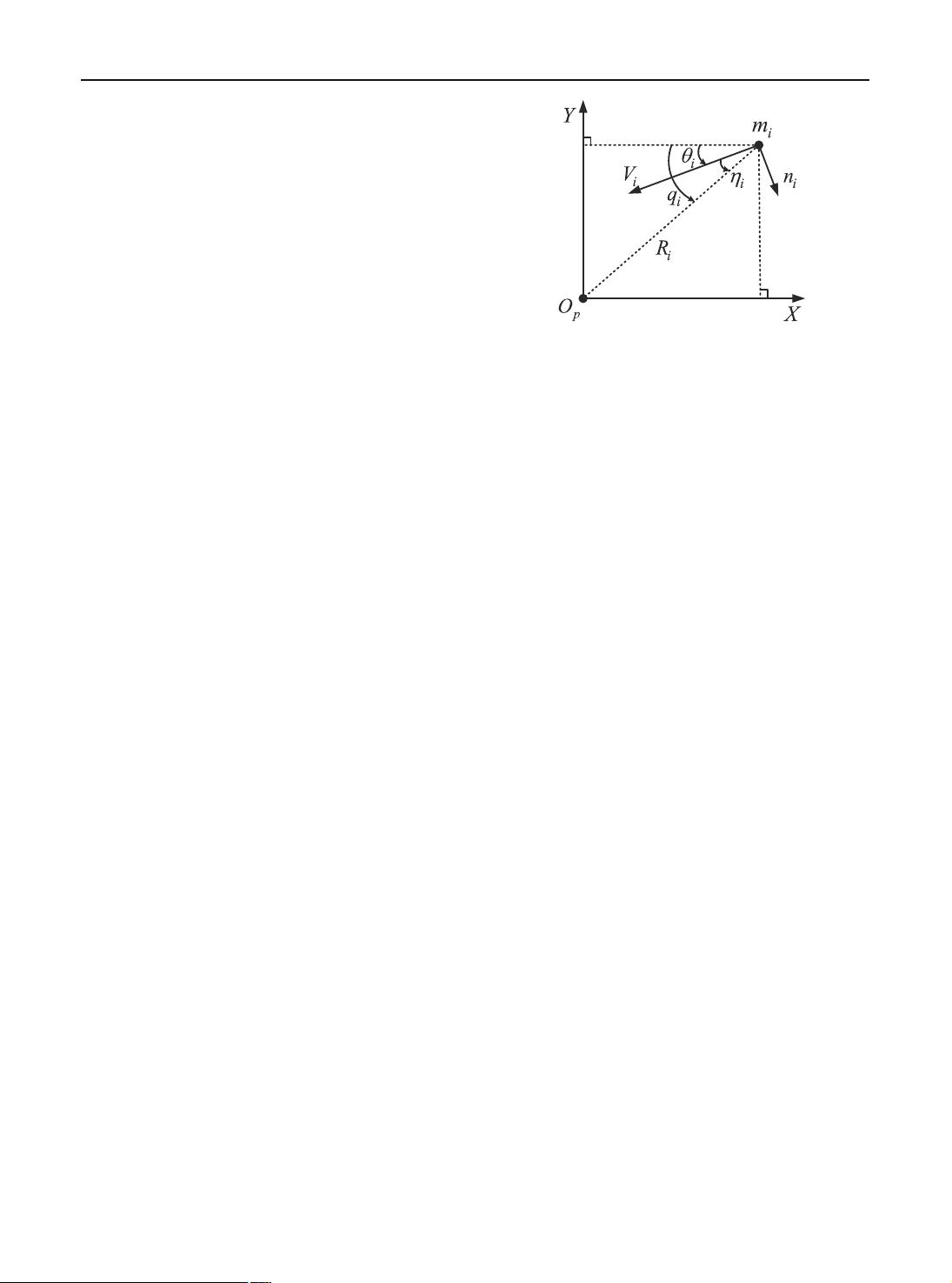
Fig. 2 Guidance geometry of m

while attacking the distinct targets. Assumption 1 is

commonly used in investigating the group behavior

problems [30–34].

Remark 3 Assumption 2 means that there exist no

cycles among multiple subgroups. By taking each sub-

group as a node, the information ﬂow among multiple

subgroups can be described by a directed graph with on

cycles. In other words, the communication structure for

multiple subgroups is a leader-following one. This kind

of communication structure is easy for application, as

was mentioned in [35,36].

Lemma 1 ([33]) Based on Assumptions 1 and 2, each

subgroup M

contains a spanning tree if and only if

Laplacian matrix L has s simple zero eigenvalues (i.e.,

L has a zero eigenvalue whose algebraic and geometric

multiplicity are both s), and the real part of all the other

(N − s) eigenvalues are positive.

2.2 Problem description

In engineering practice, the trajectory of a missile is

decomposed into motion on lateral and longitudinal

planes. This paper focuses on the lateral plane. The

following is a standard assumption when considering

cooperative guidance problems of multiple missiles

(see, e.g., [13,15,18,19,21–23,26]).

Assumption 3 (i) Both the missiles and the targets are

treated as mass points on the planar surface. (ii) Com-

pared with the guidance loop, the seeker and autopilot

dynamics of missiles are sufﬁciently fast. (iii) The axis

velocity of each missile is a constant.

The homing guidance geometry is depicted in Fig. 2.

Let m

(i ∈{1, 2,...,N }) denote the ith missile and

123

剩余16页未读，继续阅读

weixin_38581447

粉丝: 8
资源: 911

多导弹分布式协同制导：固定与切换通信拓扑策略

具有定向通信拓扑的分布式优化问题的新博弈模型

切换通信拓扑下线性多智能体系统的鲁棒协同输出跟踪控制.pdf

具有定向通信拓扑的离散时间异构多智能体系统的分布式群一致性

具有执行器故障和定向拓扑的二阶多智能体系统的分布式容错时变编队控制

定向通信拓扑下多个非完整系统的输出共识

具有定向通信拓扑的二阶非线性智能体的协调轨道跟踪控制

定向通信拓扑下一阶多智能体系统的量化共识

具有定向切换拓扑的高阶多智能体系统的自适应共识

通用定向多主体网络上的分布式收敛到鞍点

具有切换定向拓扑的无人机群系统的时变编队跟踪

最新资源