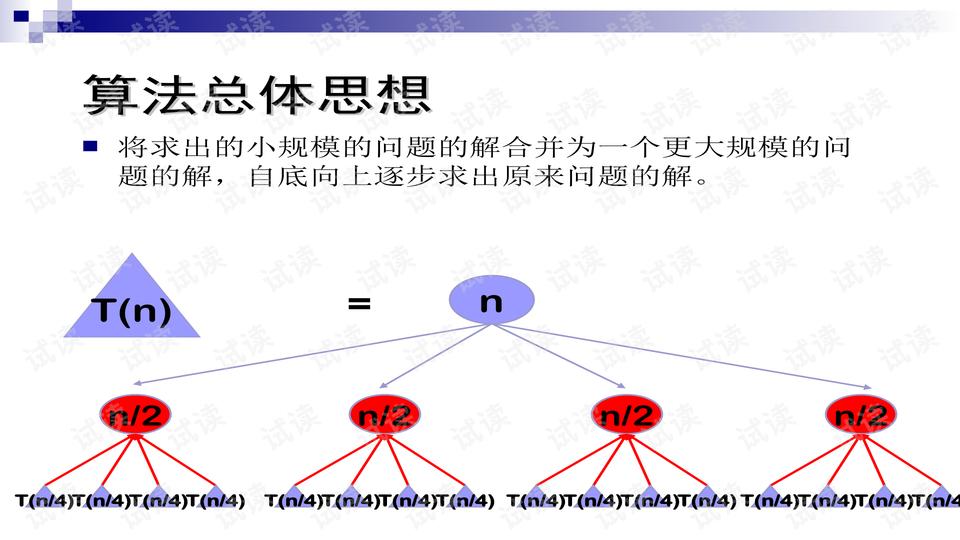
分治策略详解：线性时间选择算法

"线性时间选择算法是基于分治策略的一种高效数据处理方法，主要用于寻找序列中的第k小元素。在最坏情况下，算法的时间复杂度为O(n^2)，但在平均情况下，它可以在O(n)时间内完成任务。分治法是一种递归的解决问题的方法，将大问题分解为若干个规模较小的相同或相似的子问题，然后对这些子问题进行求解，最后将子问题的解合并，得到原问题的解。" 线性时间选择算法，也称为快速选择算法，是快速排序算法的一个变种，用于在无序的序列中找到第k小的元素。该算法的核心是分治法，它首先通过随机化选择一个基准值，然后将序列划分为小于基准值、等于基准值和大于基准值三部分。这个过程通常通过快速划分操作实现，即随机选择一个元素，重新排列序列使得所有小于基准的元素都在其左边，大于基准的元素在其右边。 算法的步骤如下： 1. 如果序列只剩一个元素，那么这个元素就是第k小的元素，返回它。 2. 如果k小于等于基准值所在位置的索引（即小于等于中间元素的位置），则在基准值左边的子序列中寻找第k小的元素，调用算法递归处理这部分。 3. 否则，在基准值右边的子序列中寻找第k减去基准位置索引加1小的元素，因为基准左边已经有k-1个小于或等于k小的元素了，所以调用算法递归处理这部分。 分治法的典型应用包括二分搜索、大整数乘法（如Karatsuba乘法和Toom-Cook乘法）、Strassen矩阵乘法、棋盘覆盖问题、合并排序和快速排序等。在这些问题中，分治法都能够将复杂问题简化为规模更小的相似问题，通过递归的方式解决。 线性时间选择算法的效率在于，虽然在最坏情况下，比如输入序列已经完全有序，它的性能退化到O(n^2)，但通过随机化选择基准，可以保证在平均情况下的时间复杂度为O(n)。这是因为随机化可以防止最坏情况的发生，使得每次划分都能平均地减少问题规模。 总结来说，线性时间选择算法是一种利用分治策略在平均情况下能够高效找到序列中第k小元素的算法，其核心是随机化的快速划分操作。通过递归地将问题分解为更小的部分并逐层解决，最终达到解决大规模问题的目的。