数据结构第六章:树与二叉树详解
需积分: 41 59 浏览量
更新于2024-07-20
收藏 3.18MB PPT 举报
"《数据结构》第六章讲义"
在数据结构的学习中,树是一种非常重要的非线性数据结构,它能够有效地模拟多种现实世界中的问题和数据组织方式。本讲义主要聚焦于树和二叉树,涵盖了以下几个关键知识点:
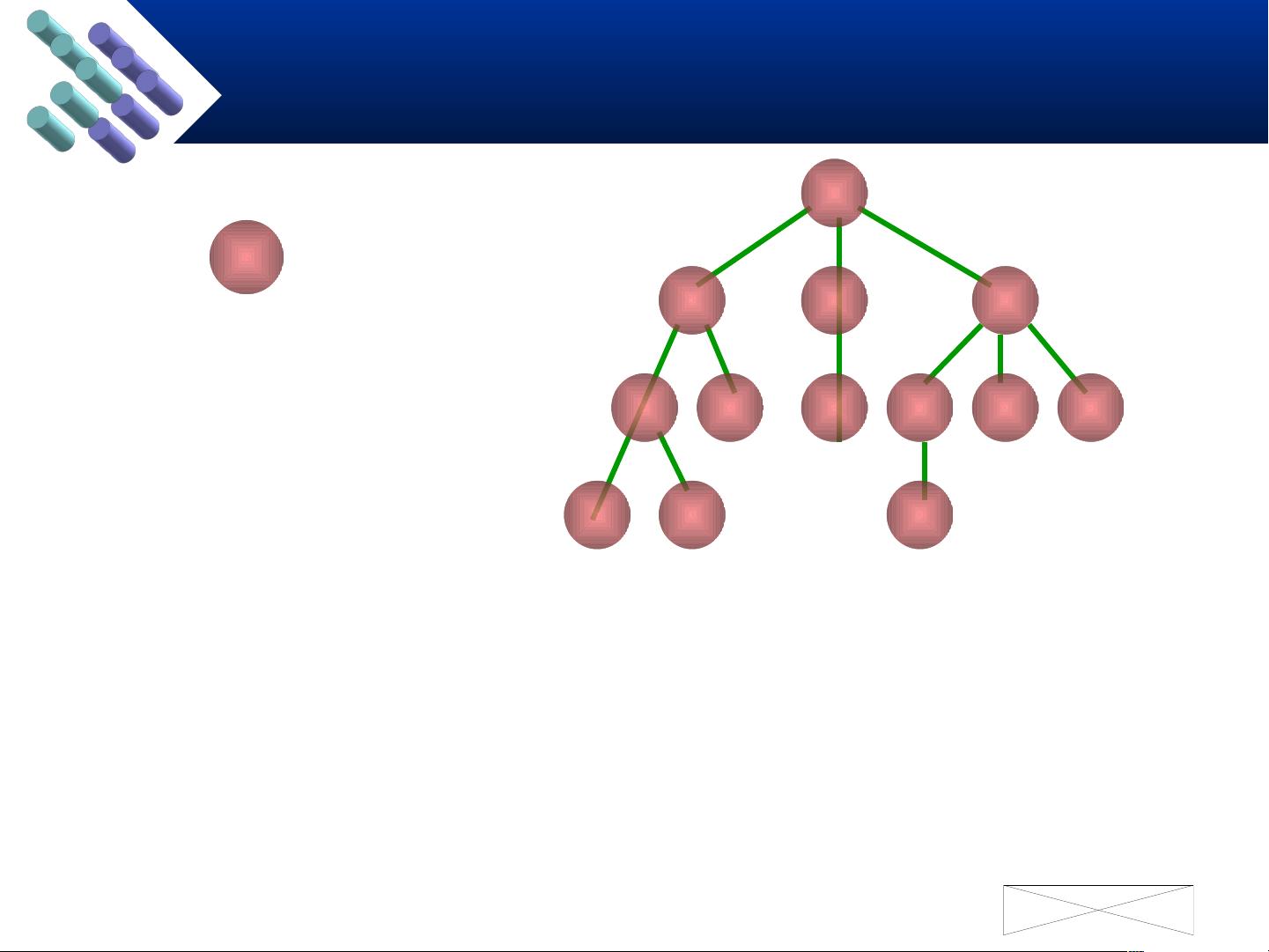
1. 树的定义和基本术语:
- 树由n个有限数据元素组成,每个元素称为结点。树的根结点没有前驱结点,而其余结点分为若干棵子树,这些子树的根结点称为父结点,相应的父结点则称为子结点。
- 结点之间通过边连接,每条边代表一种父子关系。
- 没有子结点的结点称为叶子结点或终端结点。
- 结点的度是其子树的数量,树的度是所有结点的度的最大值。
2. 二叉树:
- 二叉树是每个结点最多有两个子结点的特殊树,分为左子结点和右子结点。
- 二叉树的遍历包括前序遍历(根-左-右)、中序遍历(左-根-右)和后序遍历(左-右-根)。
- 线索二叉树是在二叉树的空链域中附加线索,以便于非递归遍历。
3. 遍历二叉树:
- 递归算法是二叉树遍历的常见方法,通过递归调用函数来访问每个结点。
- 非递归算法通常利用栈或队列实现,如 Morris遍历和BFS(广度优先搜索)。
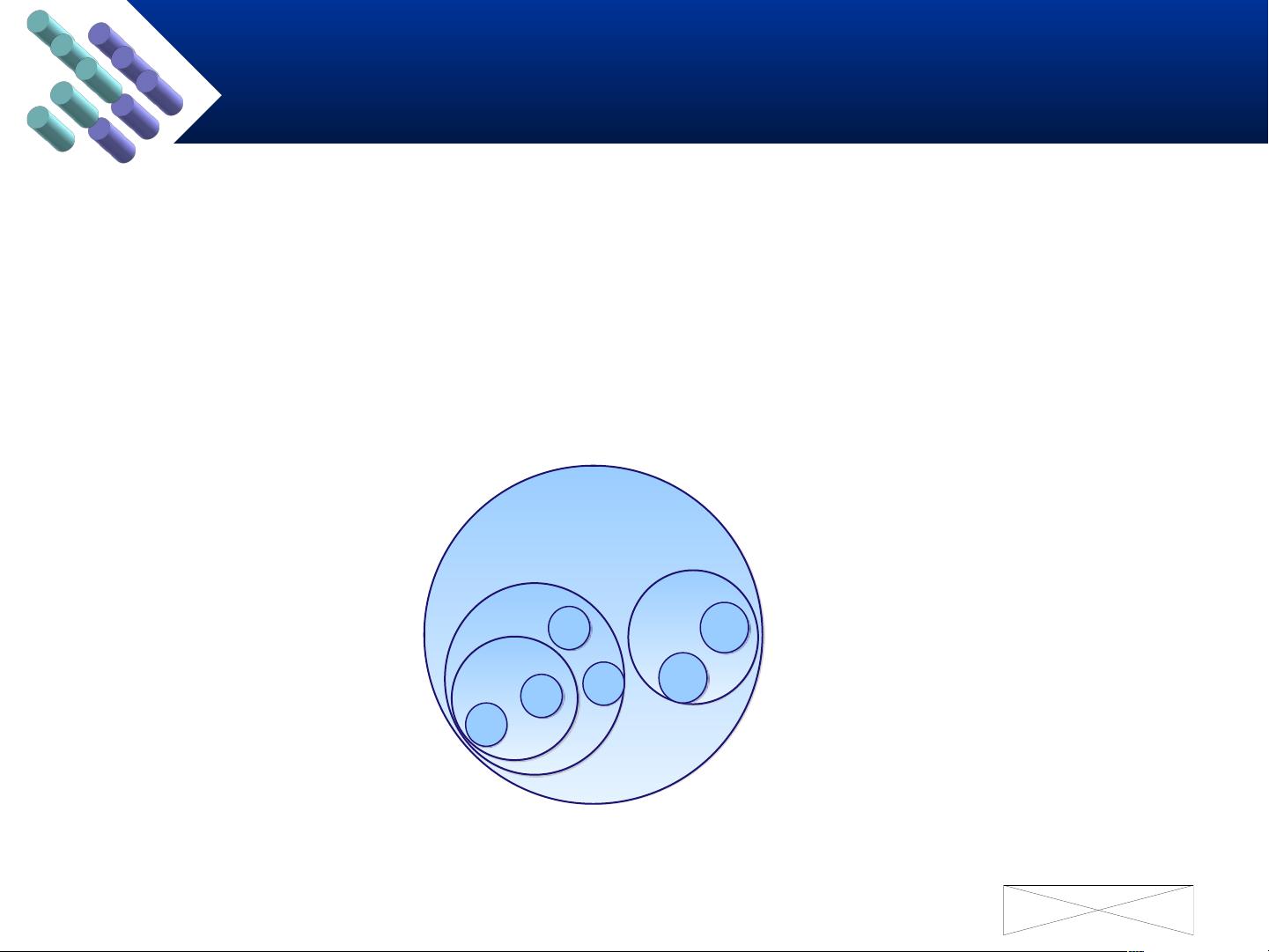
4. 树和森林:
- 树可以转换为森林,森林也可以转换为树。这种转换在处理树的合并和拆分时很有用。
- 在森林中,根结点没有父结点,而子树的根结点可以看作是森林中树的结点。
5. 赫夫曼树及其应用:
- 赫夫曼树(Huffman Tree)是一种带权路径长度最短的二叉树,也称为最优二叉树,常用于数据压缩。
- 赫夫曼编码是根据赫夫曼树生成的,它是一种变长编码,频率高的字符对应较短的编码,可以提高编码效率。
6. 二叉排序树:
- 二叉排序树(Binary Search Tree, BST)是一种二叉树,其中每个结点的左子树只包含小于该结点的结点,右子树只包含大于该结点的结点。
- BST支持快速的查找、插入和删除操作,性能取决于树的平衡程度。
学习这章内容时,应重点掌握二叉树的性质,如完全二叉树、满二叉树的概念,以及不同存储结构,如链式存储和数组存储。同时,理解二叉树遍历的递归和非递归算法,并能熟练运用到实际问题中。难点在于理解和应用二叉树的性质,以及构建最优二叉树和哈夫曼编码的方法。
通过案例分析,例如家族树可以用来理解树的结构,书的目录结构展示树如何表示层次关系,而人机对弈中的局面可以映射为树型结构,帮助我们更好地理解树和线性结构的区别。通过这些案例,可以加深对树型数据结构的理解和应用。
165 浏览量
117 浏览量
2021-08-31 上传
2021-08-31 上传
2014-03-05 上传
2016-05-26 上传
点击了解资源详情
点击了解资源详情
2012-12-28 上传
NYIST_TC_LYQ
- 粉丝: 99
- 资源: 6
最新资源
- 网络蜘蛛基本原理和算法
- 搜索引擎基本原理和算法介绍
- 计算机网络第四版(谢希仁)习题详细答案.doc
- Efficient C++ Performance Programming TechniquesAddison.Wesley.Efficient.C...Performance.Programming.Techniques.pdf
- CISCO路由器配置手册.doc
- IAR-AVR C编译器指南.pdf
- 软件工程学习书《人月神话》
- 40种网页常用小技巧
- rose ha 配置文档
- Software Architecture4+1
- 索引的SQL语句优化
- C++实现人工神经网络的类
- Qt嵌入式图形开发(入门篇)
- J2EE中文教材.doc
- 实战XML第二版.pdf
- Qt嵌入式图形开发(基础篇).pdf