基于多项式法的闭环系统极点配置与MATLAB实现

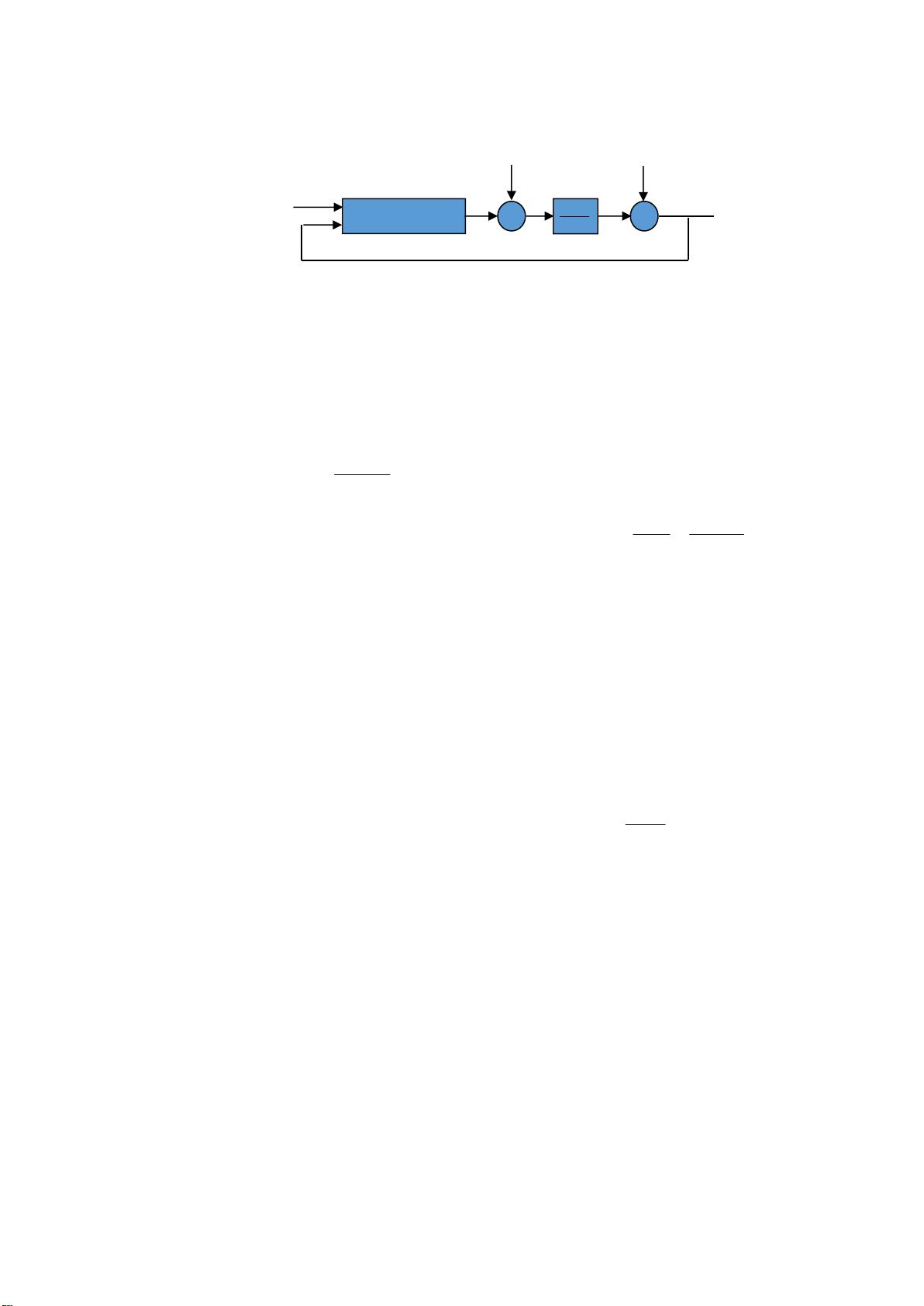
本文主要探讨了基于多项式方法的极点配置在控制系统设计中的应用，特别是在一个含有指令信号、负载扰动和测量噪声的闭环系统中。文章以大连理工大学为背景，以一个二阶系统为例进行详细分析。 首先，系统被建模为一个带有零阶保持器的采样脉冲传递函数，其中G(s)是过程模型，采样周期h设定为1秒。目标是实现期望的闭环极点位置，如0.5和0.6。为了满足这个目标，采用了一种有限拍观测器（Observer）来改善系统的性能。 控制器设计部分，首先假设控制器没有积分项，即A_c的阶数为2。根据性能规范，设计了一个丢番图方程，该方程涉及到极点位置的确定，包括系统矩阵A、观测器矩阵A_o、控制器增益矩阵R和S，以及输入矩阵B。丢番图方程通过系数的线性组合等于零来确定这些参数，例如： A * z^3 + R * z^2 + S * z + B = 0 代入特定的极点位置和观测器特性，解出各个系数。解得极点s_1 = 7.0, s_2 = 9.0, r = 0.1, 等待其他未知参数。 接着，控制律Y(s)被设计为一个多项式表达式，它结合了观测器输出Y(s), 输入U(s), 和扰动项r(s)，并通过反变换得到具体的控制律u(t)。最终的控制器结构由MATLAB源程序给出，表明了控制器如何将测量值转化为实际的控制信号，以稳定闭环系统并达到期望的性能指标。 总结来说，本文的核心内容是利用多项式方法来精确地配置闭环系统的极点，通过解决丢番图方程并结合系统模型，设计出适应特定性能需求的控制器。这部分技术在工业自动化和控制系统设计中具有重要的应用价值，尤其是在面对复杂动态环境时，优化系统的稳定性与响应速度。