鲁棒分布式定位：应对噪声的智能传感器网络算法

186 浏览量更新于2024-08-27 收藏 896KB PDF 举报

“分布式网络本地化：带有噪声测量和通信信息的准确估计” 本文深入探讨了在传感器网络中，如何在存在测量噪声和通信噪声的情况下，解决没有共享公共参考系的节点定位问题。针对这一挑战，文章提出了两种创新的算法：一种是鲁棒的分布式方向估计算法，另一种是鲁棒的分布式节点定位算法。这两种算法的设计目标是有效地抑制由噪声引起的不确定性。首先，鲁棒分布式方向估计算法旨在处理由于测量设备不精确或环境干扰导致的方向测量误差。通过构建无偏估计器，该算法能够利用历史测量信息来校正测量噪声的影响，从而提高方向估计的准确性。其次，为了降低通信噪声对定位精度的影响，文章引入了随机逼近方法。这种方法允许传感器节点在网络中逐步调整其估计位置，以更接近实际位置，即使在通信链路质量不稳定的情况下也能保持稳健。论文进一步假设测量噪声和通信噪声具有零均值和独立性，这是许多统计分析的基础。在这种情况下，作者证明了一个关键的理论结果：只有当网络包含至少一个已知位置的“锚节点”时，所有的传感器节点才能在设计的算法下几乎确定地渐近确定它们自己的方位角和位置。这种网络结构要求通信和距离传感拓扑以锚节点集为根，并且连接了相应的方位传感拓扑，以确保信息的有效传递和处理。此外，论文还讨论了在仅考虑测量噪声或通信噪声的特殊情况下，算法的收敛速率。这为理解和优化算法性能提供了定量依据。通过一系列的仿真实验，验证了所提出的算法在实际应用中的有效性和效率，证明了其在有噪声环境下的强大适应性。这项工作对于理解和解决传感器网络中的本地化问题具有重要的理论价值和实践意义，特别是在存在多种噪声源的复杂环境中。它为未来的研究提供了新的思路，包括改进噪声抑制技术、优化网络拓扑设计以及开发更加适应现实世界挑战的定位算法。

WANG AND TIAN: DISTRIBUTED NETWORK LOCALIZATION: ACCURATE ESTIMATION WITH NOISY MEASUREMENT 5929

Fig. 1. The relative position measurement under the case that all nodes share

a common reference frame.

network is described by digraph G = {V, E, A}, and its bearing-

sensing topology is described by

G, the undirected graph induced

from G.

We denote by p

∈ C,i ∈Vthe accurate position of node i

in a global or called common coordinate system denoted by Σ

Denote by V

= {1,...,s} the set of anchor nodes whose po-

sitions p

,i∈V

, are known. Denote by V

= {s +1,...,N}

the set of sensor nodes whose positions p

,i∈V

aretobe

determined. Each node i ∈V

makes and records its all mea-

surements with respect to its own local coordinate system Σ

whose origin is assumed to be just at the position of node i, and

whose orientation with respect to Σ

is a constant denoted by

∈ (−π, π]. θ

is assumed to be unknown for each sensor node

i ∈V

. We call all nodes share a common reference frame, if

directions of the coordinate axis of each node’s local coordinate

system are the same as ones of the common coordinate system

(i.e., θ

=0, ∀i ∈V). As for the anchor, since its position in Σ

is known, we set its orientation θ

=0, ∀i ∈V

, without loss of

generality.

Firstly, we assume all nodes share a common reference frame.

Then, as shown by Fig. 1,

= p

− p

(1)

is the relative position of j measured by node i, which can be ex-

pressed as b

= |b

ıδ

with δ

∈ (−π, π] denoting the bear-

ing of node j in Σ

. In practice, the relative position information

can be obtained by the node through the distance measurement

and bearing measurement, where an alternative distance mea-

surement method is the time of arrival (TOA) method (see, e.g.,

[2]) and the bearing can be measured by a bearing measurement

sensor, such as a camera (see, e.g., [21]) or an antenna array (see,

e.g., [22]). Let b

be the weighted sum of the relative positions

of all the node i’s neighbors measured by node i, i.e.,



j∈N

. (2)

For all anchor nodes, we let b

=0, ∀i ∈V

. Then, we can

aggregate (1) and (2) for all nodes into the following form

−Lp = b, (3)

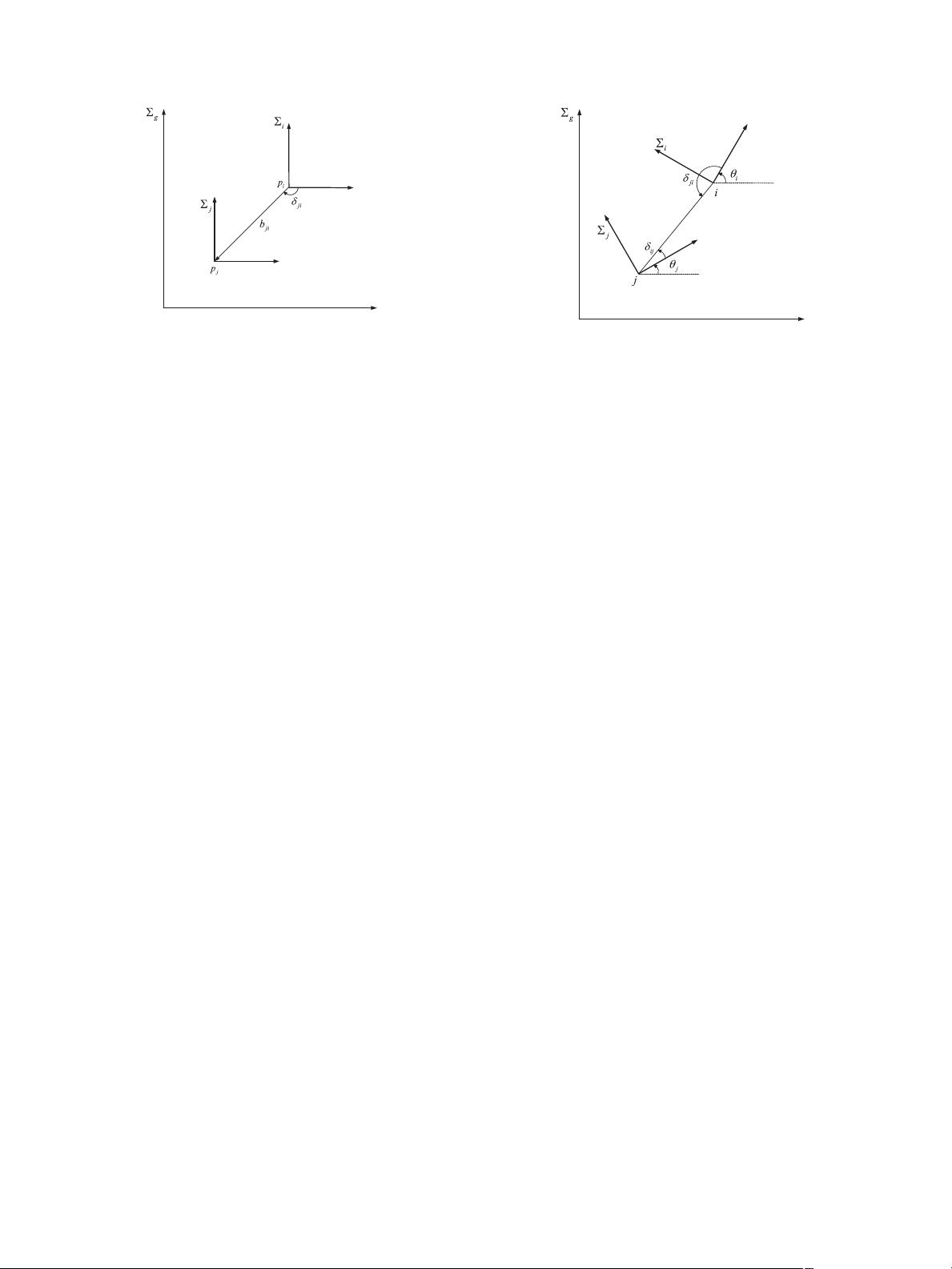
Fig. 2. The bearing measurement in local coordinate systems and orientations.

where L is the Laplacian matrix of G(A) with partition L =

[

], p =[p

,...p

]

, b =[b

,...,b

]

Obviously, to ensure the localizability of the network with

relative position measurements, L

should be i nvertible. By

Lemma 3.1 given in [23], we know that the non-singularity of

is guaranteed if and only if the relative position sensing

topology G is 1-rooted at the anchor node set. A distributed

iterative localization algorithm can be constructed as

ˆp

(t +1)= ˆp

(t)+c



j∈N

(ˆp

(t) − ˆp

(t) − b

),i∈V

(4)

where t ∈ N, c is a small positive constant to be designed,

ˆp

∈ C,i ∈V

denotes estimate of the position p

made by

node i at the tth iteration. Let ¯p

(t)=[¯p

(t),...,¯p

(t)] with

¯p

(t)=ˆp

(t) − p

, ∀i ∈V. By (1), Eq. (4) together with ¯p

(t) ≡

0, ∀i ∈V

, can be aggregated into

¯p(t +1)=(I − cL)¯p(t).

(5)

Now, we can see that the relative-position based node-

localization problem with multiple anchor nodes can be trans-

formed into a consensus control problem with multiple leaders

at the same positions [23], [24].

Then, we consider the case that all nodes do not share a

common reference frame, which implies that there are some

nodes i ∈V

such that θ

s are unknown and θ

=0in general

(see Fig. 2). In this case, p

− p

is no longer equal to b

, and

instead, we have

− p

= e

ıθ

. (6)

In order to achieve the node-localization, each sensor node i ∈

needs to determine its own orientation θ

(or the orientation

vector e

ıθ

) ﬁrst and then determine its position in the common

coordinate system.

Denote the relative bearing μ

= δ

− δ

and deﬁne the

relative orientation

= PV(θ

− θ

), (7)

with PV(θ

− θ

)

=[(θ

− θ

+ π)mod2π] − π. The follow-

ing lemma, which is a restatement of the result of [16], shows the

relation between the relative orientation and the relative bearing.

剩余13页未读，继续阅读

weixin_38540819

粉丝: 7
资源: 830

鲁棒分布式定位：应对噪声的智能传感器网络算法

MATLAB代码：分布式最优潮流 关键词：网络划分；分布式光伏；集群电压控制；分布式优化；有功缩减 参考文档：含分布式光伏的配

编写分布式的Erlang程序：陷阱和对策

具有通信和测量噪声的传感器网络中的分布式本地化

分布式控制状态估计：间歇测量的稳定性和精度分析

Java分布式系统通信详解：模块拆分与通信策略

分布式鲁棒自适应控制：应对复杂网络通信不完美的策略

分布式系统深入解析：NFS与进程通信

安捷伦J6801A分布式网络分析仪：高效测试解决方案

分布式系统理论精要：异步计算与同步通信

分布式操作系统详解：通信与资源管理

最新资源

MATLAB代码：分布式最优潮流关键词：网络划分；分布式光伏；集群电压控制；分布式优化；有功缩减参考文档：含分布式光伏的配