华罗庚数学：导数应用详解与极值分析

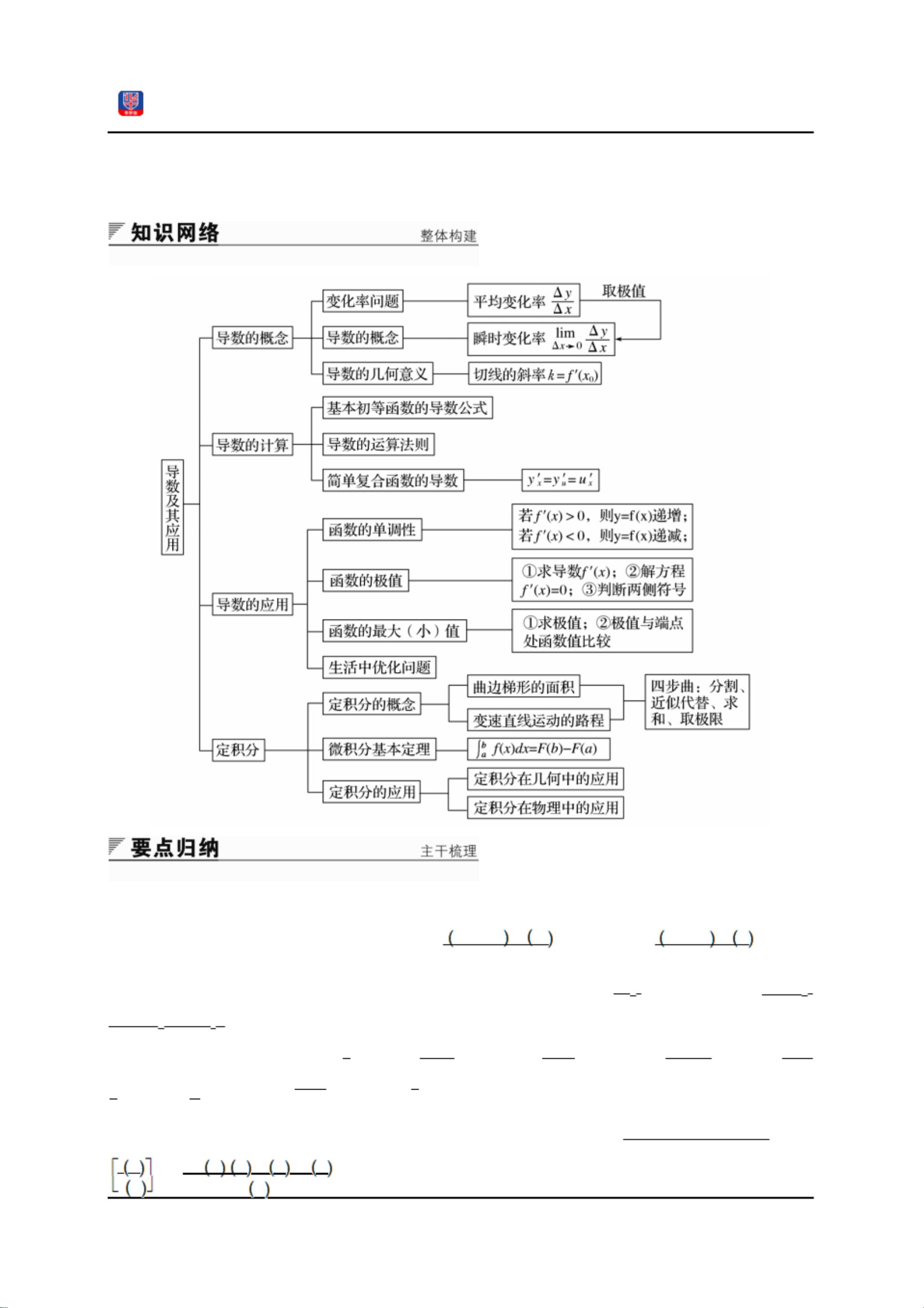
本资源是一份名为"同步讲义8 - 导数及其应用复习课(理).pdf"的讲义，主要针对高中或大学阶段的数学课程，尤其关注导数的概念、运算及其在实际问题中的应用。讲义首先介绍了导数的定义和基本概念，包括： 1. 函数f(x)在某点x0处的导数定义，即导数是函数值变化率的极限表示，它给出了曲线在该点切线的斜率。 2. 几何意义：导数等于曲线在该点的切线斜率，切线方程的表达式也包含在其中。 3. 提供了常用的导数计算公式，如常数函数、幂函数、三角函数、指数函数和对数函数的导数，以及导数的四则运算法则。 接下来，讲义深入探讨了导数的应用，涉及函数的单调性分析、极值和最值的判断，以及如何运用导数解决生活中的优化问题。例如，通过比较导数的符号变化来确定函数的增减区间，寻找函数的极值点，并利用这些极值来确定闭区间上的最值。 特别地，资源还涉及定积分的概念，包括解决与切线相关的实际问题，如例1中求解函数e^x - ax的切线问题。该例子不仅要求出a的值和函数的极值，还通过分析证明了一个关于指数函数的不等式。 此外，讲义还提到了高考中常见的求切线方程问题的两种类型，一种是在特定点处求切线，另一种是利用导数的性质进行求解。这部分内容对于理解导数的实际应用和解题技巧至关重要。 这份讲义为学生提供了全面而深入的导数理论和实际应用知识，适合备考学生或自我提升者学习和复习。通过掌握这些内容，学生将能够更好地理解和解决与导数相关的数学问题，提升数学分析和解决问题的能力。