简化版土体饱和塑性本构模型解析

需积分: 10 125 浏览量更新于2024-07-22 收藏 1.81MB PDF 举报

"《关键土壤力学模型：Alonso-Gens-Josa的理论》本文档探讨的是土体的经典本构模型，特别适用于岩土工程领域的初学者。作者E.E. Alonso、A. Gens和A. Josa在1990年的《GCotechnique》杂志上发表了一篇论文，提出了一种名为“部分饱和土壤的应力-应变行为描述模型”。该模型基于硬化塑性理论，采用两种独立的应力变量来刻画土体特性：总应力与大气压力之差（称为过应力）以及吸力（ suction）。模型设计的核心理念是将之前分别处理的部分饱和土壤的各种基本行为，如压缩性、膨胀性、水分迁移等，以一种一致且统一的方式进行描述。它强调了在未达到饱和状态时，模型能够展现出复杂的行为特征，而一旦土壤达到饱和，模型则过渡到经典的临界状态模型。这样的设计考虑了实际应用中的实用性，尽量保持简单以便后续的扩展研究。论文着重展示了模型在各向同性和双轴应力状态下的一般预测，并针对轻微或中度膨胀的土体进行了典型的应用讨论。作者们意识到，尽管实验数据仍不充分，但他们的模型为理解和模拟这部分土壤提供了基础框架，为后续的深入研究和工程实践提供了重要的工具。通过学习和理解Alonso-Gens-Josa提出的这个模型，初学者能够更好地掌握部分饱和土壤的力学行为，对于理解土体在建筑物地基、地下水管理和地质灾害防治等领域的响应具有重要意义。进一步的模型改进和参数校准可根据具体工程项目的特性进行，以提高预测精度和工程设计的可靠性。"

CONSTITUTIVE MODEL FOR PARTIALLY SATURATED SOILS

409

J, (0)

Collapse

‘\I

s=o

(b)

Fig. 2. Relatioasbip between preconsolidation stresses pO nod

po*: (a)

compression

carves for saturated and uasatorated soil; (b) stress path and yield carve in (p, s) stress

plane

and 2(b)). The following identity may be estab-

lished

v1 + Au, + Au, = vj

(3)

where the different quantities are indicated in Fig.

2(a).

The suction unloading (wetting) from 2 to 3

occurs in the elastic domain. Under these circum-

stances a reversible swelling Au, takes place which

is given by a logarithmic expression similar to

Equation (2)

dv=

-K,-

(s +

P.3

(4)

pa,

has been added to s to avoid infinite values as

s approaches zero.

Taking into account Equations (l), (2) and (4),

Equation (3) becomes

s + Pat

N(s) - L(s) In F + K In G + ic, In -

P.t

= N(O) - I(O) In 5

(5)

which provides a relationship between

and s as

a function of some reference stress values

(PO*, p’)

and some soil parameters (N(s), n(s),

K, K,).

A con-

venient choice of

and N(s) to simplify Equation

410

ALONSO, GENS AND JOSA

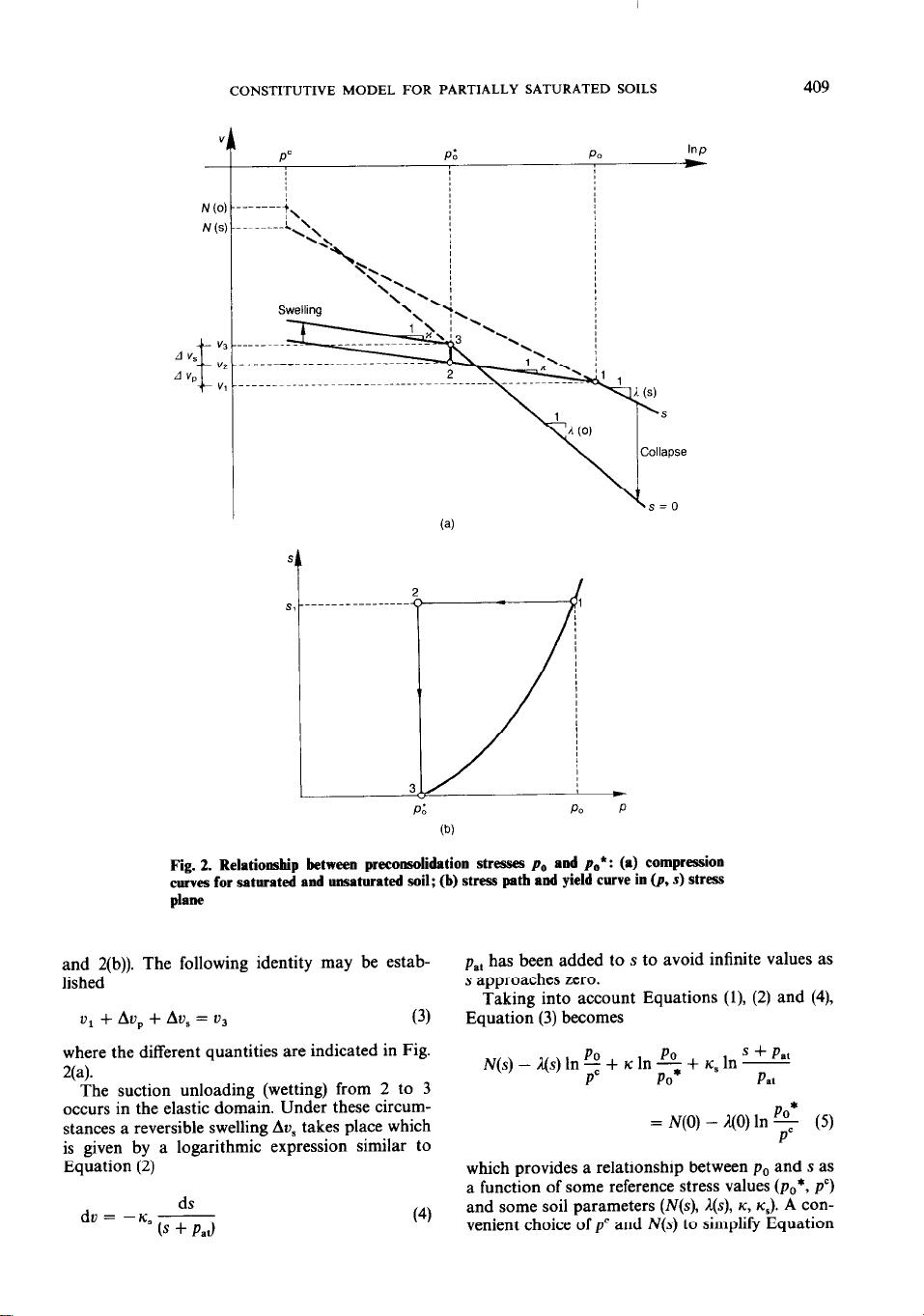
(5) is to assume (Fig. 2(a))

s +

Pat

A~(p”)l,~ = N(0) - N(s) = K, In -

(6)

P.1

In other words,

p’

is the net mean stress at which

one may reach the saturated virgin state, starting

at a partially saturated condition, through a

wetting path which involves only (elastic) swell-

ing.

If Equation (6) is introduced into Equation (5),

the following relationship is obtained

@) =

(&_qo)-Kl/wKl

This Equation defines the set of yield

values

for each associated suction (it can be considered

therefore as a family of yield curves in a (p, s)

space). In order to isolate a single yield curve it is

necessary to specify the preconsolidation net

mean stress for saturated conditions

(po*)

which

may be viewed as the hardening parameter in

Equation (7). This Equation plays a central role

in the model developed and explains, as discussed

at length later, not only the apparent increase in

preconsolidation stress associated with increasing

suction,

but also the collapse phenomena

observed in wetting paths. For this reason, the

yield curves (7) will be named LC yield curves

(after loading-collapse). An LC yield curve

through points 1 and 3 has been sketched in Fig.

2(b). Note that when

po* =

the LC yield curve

becomes a straight line

(p. = p’).

In this case,

changes in s do not result in plastic deformations.

Only the elastic component, as given by Equation

(4), is maintained.

Existing information on the volumetric behav-

iour of partially saturated soils, as revealed by

suction controlled tests, may be used to support

some of the model assumptions. The results of a

number of isotropic and oedometer tests of this

type were compiled by Lloret & Alonso (1985)

and reported in terms of state surfaces (the void

ratio was expressed as a function of net vertical

or net confining stress and suction). Surface fitting

analysis was performed in order to find the most

appropriate analytical expression for the analysed

data. The tests considered involved different soil

types (low plasticity clays, silty clay and clayey

sand) and suction values ranging from zero to 100

kPa in most of the cases.

Most of the reported state surfaces have been

obtained through stress paths which involve

reductions in suction from an initial value and a

subsequent increment in net mean (or vertical)

stress

A path of this kind is shown in Fig. 3.

For this particular path, the final specific volume

for the (generic) stress state (p, s) may be written

St__--------_

~.~~~~~__~~~~~~

Fig. 3. Wetting and loading stress path in (p, s) stress

plane

ufp,

s) =

v(p’, si) + Au(p”) ’ + l(s)

In s

(8)

where the p-loading was supposed to take place

along virgin states. This expression may be com-

pared with the following empirical equation

which was found by Lloret & Alonso (1985) to fit

well experimental results

v=a+bln$+clns+dln4lns

= a + c In s + (b + d In s) In !-

(9)

where

a, b, c

and

are constants.

Identifying Equations (8) and (9) suggests that

V(P”, SJ + Av(p”) ’ = a + c In s

(10)

which supports the logarithmic variation of v

with suction adopted in Equation (6).

In addition Equation (9) provides an expres-

sion describing the increase in soil stiffness with

suction:

a(s) =

b +

d In s

(11)

This expression may adequately predict an

increase in soil stiffness with suction if

d < 0.

predicts, however,

an unlimited increase in

stiffness for increasing s and this is a limitation

for wide ranges of suction changes.

An asymptotic maximum stiffness, which is

probably closer to real behaviour, is predicted by

the alternative equation

n(s) = d(O)[(l - r) exp (-Bs) +

(12)

where

is a constant related to the maximum

stiffness of the soil (for an infinite suction),

r = l(s + co)/l(O),

and B is a parameter which

剩余25页未读，继续阅读

muqingyi66

粉丝: 0
资源: 1

简化版土体饱和塑性本构模型解析

System Mechanic Pro中文版V**.*.*.**：综合系统维护与优化解决方案

System Mechanic Ultimate Defense：全方位PC保护与性能提升工具

PROE-MECHANIC运动分析教程：实例与步骤详解

Mechanic

mechanic_shop:Mechanic_shop

mechanic-push

mechanic-docs

Sound-mechanic

Java Mechanic-开源

continuum mechanic.zip

最新资源

System Mechanic Pro中文版V**...**：综合系统维护与优化解决方案