MATLAB实现离散信号生成与图形显示

"该文档是关于使用MATLAB生成和显示常见离散信号的实验指导，包括单位抽样序列、单位阶跃序列、正弦序列、复正弦序列和指数序列。实验旨在帮助用户深入理解这些离散信号，并通过编程实践探讨它们的特性，特别是复指数序列的周期性。" 实验涉及的MATLAB函数和离散信号详细说明如下： 1. **单位抽样序列**： 单位抽样序列通常表示为δ(n)，在MATLAB中可以通过`zeros()`函数来创建。例如，要生成长度为11的单位抽样序列，可以定义`n=0:10`，然后`x1=[1 zeros(1,10)]`。如果要延迟k个单位，如延迟8个单位，可以定义`x2=[zeros(1,8) 1 zeros(1,8)]`。 2. **单位阶跃序列**： 单位阶跃序列u(n)在MATLAB中可以使用`ones()`函数生成。比如，`n=0:10`，`u=[ones(1,11)]`，将创建一个全1向量表示单位阶跃序列。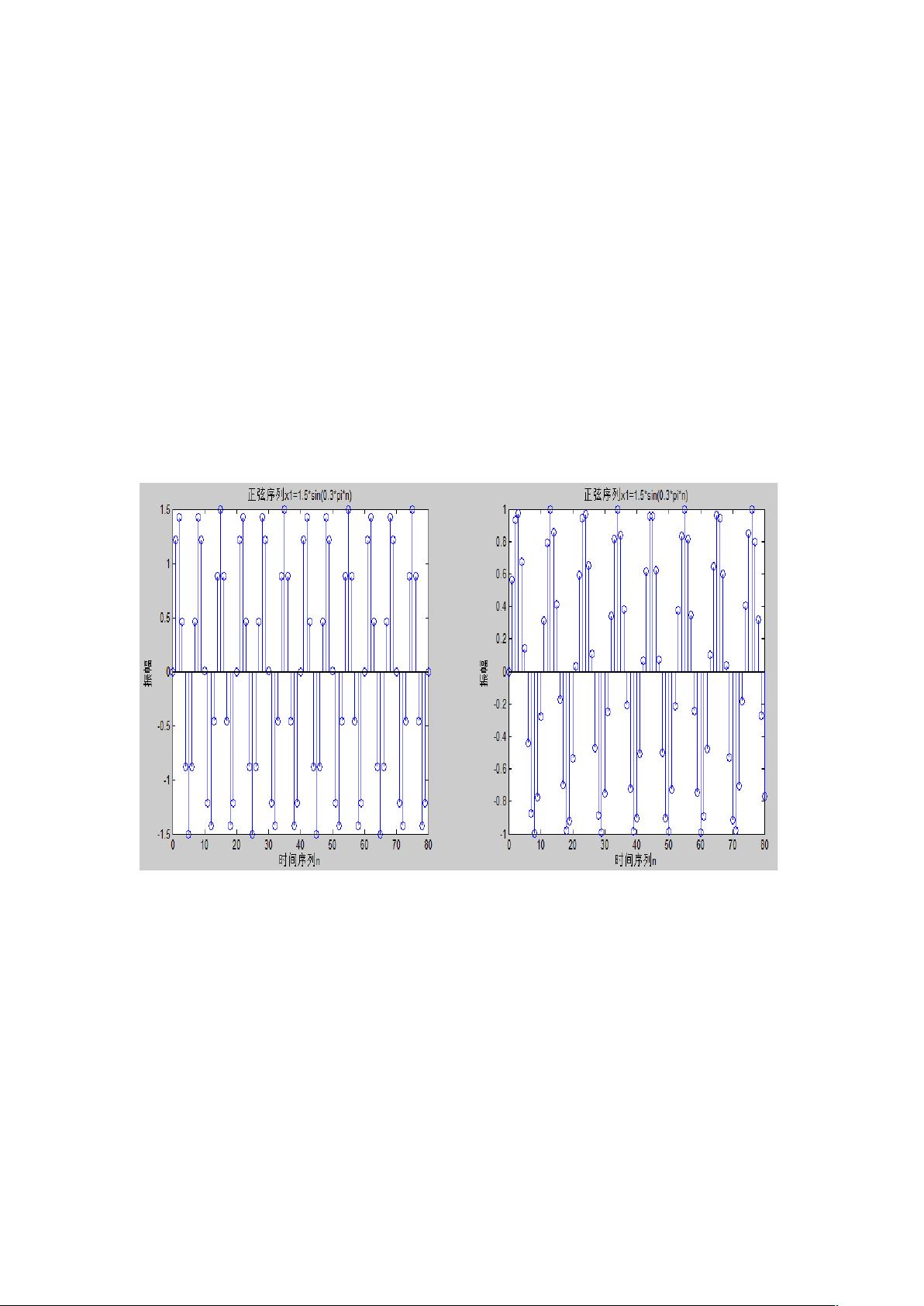 3. **正弦序列**： 正弦序列x(n)可以通过数学公式来创建，例如`x=2*sin(pi*n/6+pi/4)`。这里的`n=1:30`定义了时间轴，`pi*n/6+pi/4`是频率和相位偏移。使用`stem()`函数绘制时，可以观察到正弦波形。 4. **复正弦序列**： 复正弦序列x(n)是包含实部和虚部的正弦序列，MATLAB中的表达式如`x=5*exp(j*3*n)`，其中`j`是虚数单位，`3*n`代表角频率。此序列在复平面上呈现螺旋状，`stem()`函数绘制的是其实部和虚部的绝对值。 5. **指数序列**： 指数序列x(n)如`x=1.8.^n`，随着n的增长，序列会按照指数规律增长或衰减。`.^`操作符在MATLAB中表示元素级乘方。 实验要求用户探讨复指数序列的性质，这通常涉及到序列的周期性、频率分量以及与傅里叶变换的关系。复指数序列`x=5*exp(j*3*n)`中，`exp(j*wn)`的部分代表了一个复频率，这里的`w`是角频率，`n`是时间变量。复指数序列在傅里叶分析中具有重要意义，因为它可以分解为无穷多个正弦和余弦序列的线性组合。 通过这些实验，学习者不仅可以掌握如何在MATLAB环境中生成各种离散信号，还能直观地理解这些信号的图形表现，进而深入理解数字信号处理的基础概念。这对于学习通信、信号处理和控制系统等相关领域的学生至关重要。