数字通信第五版解答手册

"Digital Communications, 5th Edition 解答手册" 本资源是数字通信领域的一份解答手册，针对《Digital Communications》第五版的习题提供了解析，由Kostas Stamatiou在2008年1月11日编纂。这本书的内容涵盖了数位通讯的各个方面，包括信号处理、传输、噪声影响以及通信系统的建模等。 在解答手册的第二章中，讨论了关于数字通信的基础概念和分析方法。问题2.1涉及到信号的傅里叶变换和希尔伯特变换。 a. 部分内容展示了傅里叶逆变换的性质。给定信号 \( x(t) \)，其傅里叶逆变换 \( \hat{x}(t) \) 定义为 \( \frac{1}{\pi} \int_{-\infty}^{\infty} x(a) \cdot e^{j2\pi at} da \)。证明了 \( -\hat{x}(-t) \) 实际上等于 \( \hat{x}(t) \)，通过变量替换 \( b = -a \) 并利用信号 \( x(t) \) 的对称性 \( x(b) = x(-b) \)。 b. 类似地，部分b进一步证实了傅里叶逆变换对于实信号的奇偶性，即对于任何实信号，其傅里叶逆变换仍是其自身的共轭。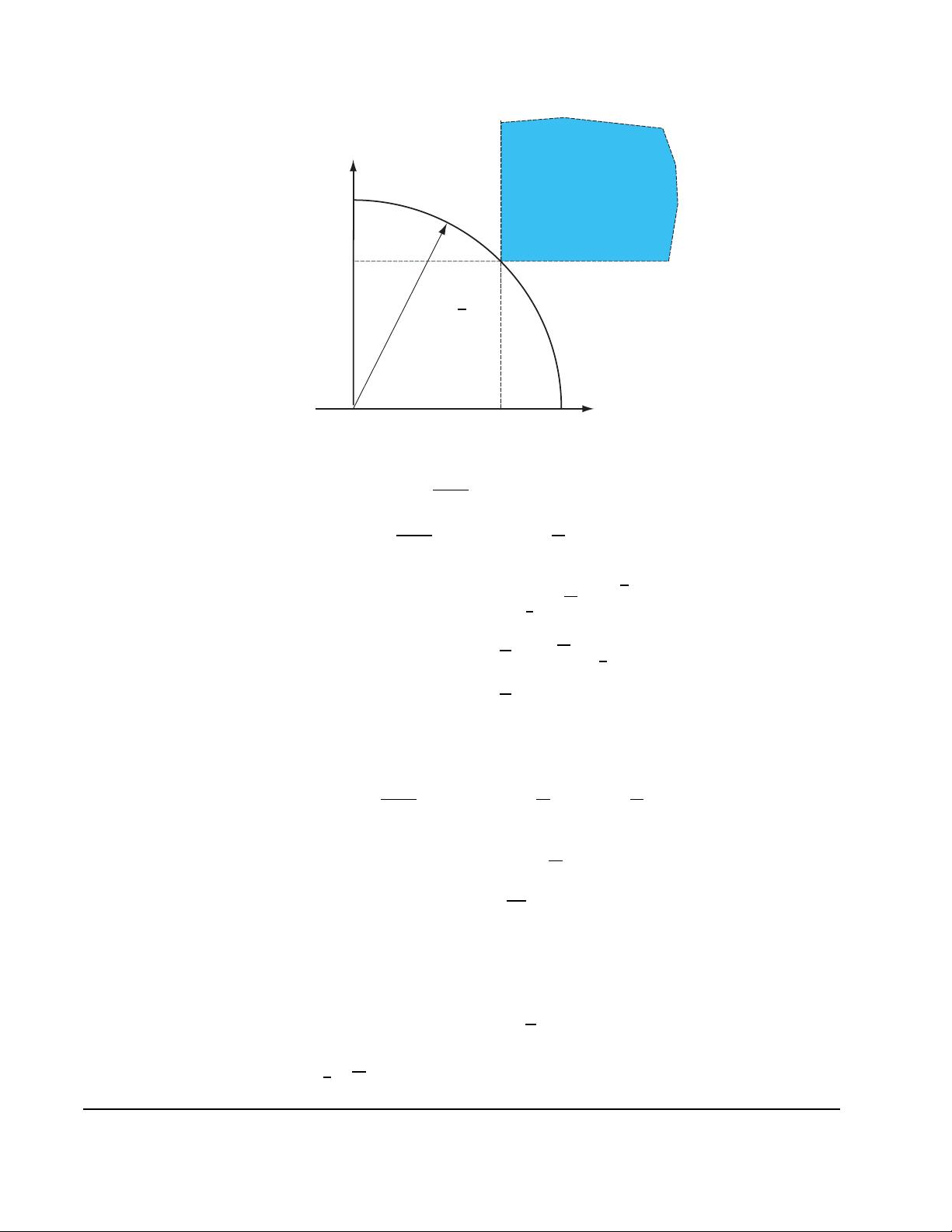 c. 这部分涉及特定的信号 \( x(t) = \cos(\omega_0 t) \) 及其傅里叶变换。\( x(t) \) 的傅里叶变换为 \( X(f) = \frac{1}{2}[\delta(f - f_0) + \delta(f + f_0)] \)，其中 \( f_0 = 2\pi\omega_0 \)。接着，利用希尔伯特变换的相移特性(2-1-4)来求解其希尔伯特变换 \( \hat{X}(f) \)，得到 \( \hat{X}(f) = \frac{1}{2j}[\delta(f - f_0) - \delta(f + f_0)] \)，这是频率为 \( f_0 \) 的正弦函数 \( \sin(2\pi f_0 t) \) 的傅里叶逆变换。 这些内容揭示了数字通信中信号处理的基本原理，包括傅里叶变换在分析周期信号中的作用，以及希尔伯特变换如何用于提取信号的瞬时相位。这些工具在实际通信系统设计中至关重要，比如在调制、解调和信道均衡等环节。通过理解这些问题的解决方案，学生和专业人士可以更深入地了解数字通信系统的工作原理。