GBDT入门详解:残差拟合与决策树增强
需积分: 9 134 浏览量
更新于2024-07-17
1
收藏 4.23MB PPTX 举报
GBDT (Gradient Boosting Decision Tree) 是一种强大的机器学习算法,尤其适用于回归和分类问题。它起源于Friedman的论文「Greedy Function Approximation: A Gradient Boosting Machine」,将梯度下降法、Boosting方法和决策树技术结合在一起。GBDT的核心思想是通过迭代的方式,每一步构建一棵弱决策树来预测残差,从而逐步改进整个模型的性能。
**决策树基础**
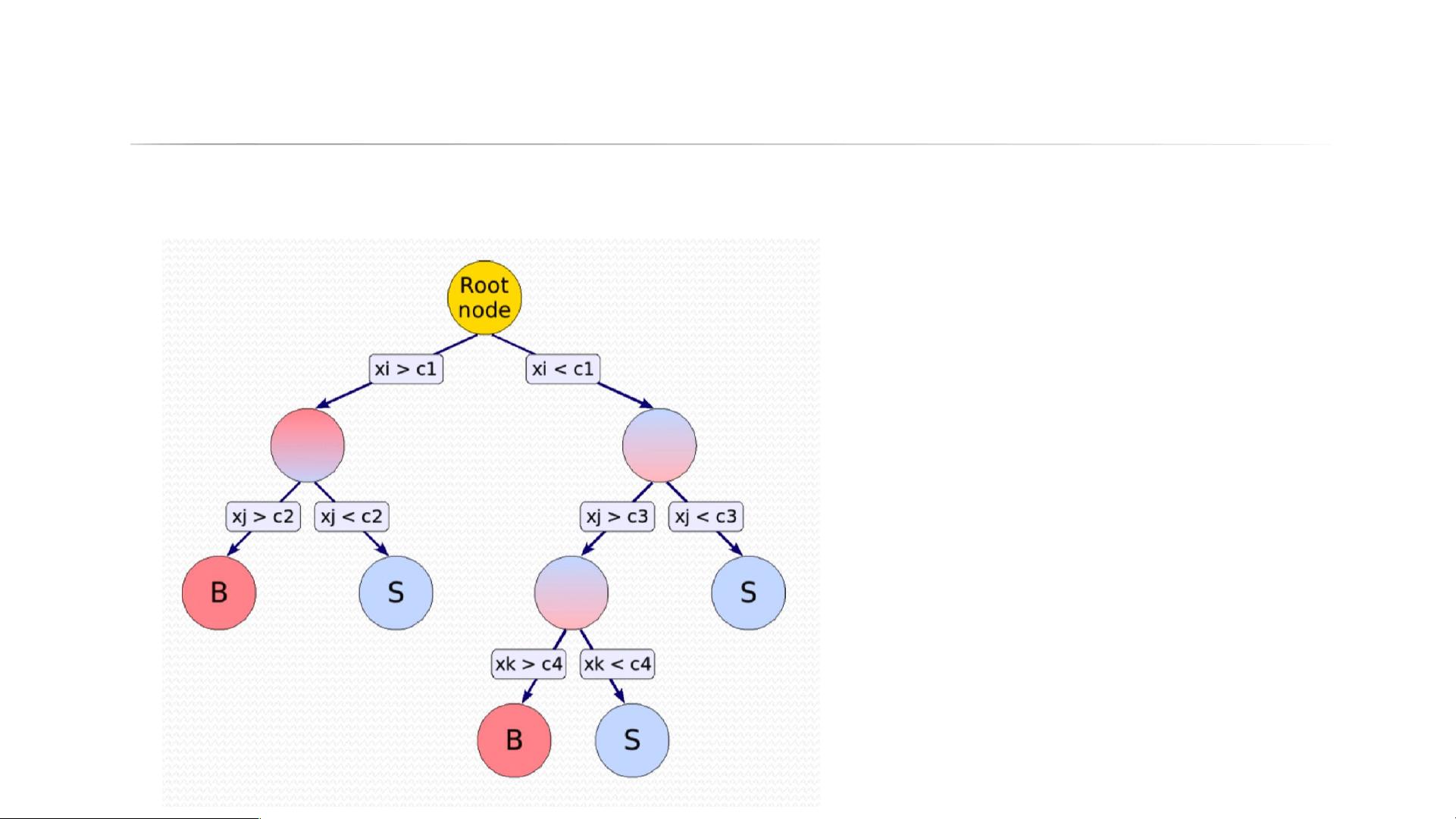
决策树是GBDT中的基本组件,用于将特征空间划分为多个子区域。分类树用于分类任务,通过超平面划分决定样本属于哪个类别;回归树则用于预测数值型目标,通过连续的划分来最小化预测误差。决策树具有很强的可解释性,能处理混合类型特征,且能自然处理缺失值,对异常点有一定鲁棒性。
**Boosting原理**
Boosting是一种集成学习方法,通过累积多个弱分类器(如决策树)形成一个强分类器。它关注如何调整每次迭代中训练数据的权重,以优先关注那些先前预测错误的样本。这有助于减少模型的整体偏差,提高整体性能。
**GBDT流程**
GBDT流程包括以下步骤:
1. 初始化:选择一个基模型(如随机森林或单棵树),进行初步预测。
2. 计算残差:使用当前模型的预测结果与实际值之间的差异作为下一轮训练的目标。
3. 构建新树:针对残差进行训练,构建一棵新的决策树,尽可能减小残差。
4. 更新模型:将新树加入模型中,通过加权平均的方式组合所有树的预测。
5. 重复迭代:直到满足预设的停止条件(如达到预定的树的数量或验证集上的性能不再提升)。
**正则化和损失函数**
为了防止过拟合,GBDT引入了正则化机制,通过控制树的复杂度,例如限制树的最大深度或节点数。损失函数的选择也对性能有很大影响,常见的有平方损失(用于回归)和逻辑损失(用于分类)。
**梯度下降法的应用**
GBDT利用梯度下降法在函数空间中优化模型,而非传统的参数空间。它通过计算损失函数关于模型预测的梯度,确定每个节点分裂的最佳特征和阈值,以此进行决策树的构造。
GBDT是一种有效的机器学习工具,特别适合处理非线性和不规则的数据分布,但需要注意的是,高维稀疏数据可能会降低其效率,而且对数据质量敏感。理解GBDT的原理、流程以及正则化和损失函数的选择,是入门和深入学习的关键。
522 浏览量
2025-01-08 上传
2025-01-08 上传
2025-01-08 上传
Ricky杨旭东
- 粉丝: 0
- 资源: 1
最新资源
- SocketCode.7z
- Xiaomi-MACE-Notes
- dbxincluder:带有XInclude 1.1的DocBook的内含物
- 电信设备-基于手机短信实现远程开门的系统及方法.zip
- OMDB:打开电影数据库
- jessie-ffmpeg:jessie-ffmpeg-使用ffmpeg和imageMagik创建Docker映像
- 模拟退火算法解决tsp问题.rar
- 年度业绩、能力盘点清单(总经理)
- Stripe-crx插件
- BiologyCalculator:IT-планета2021年的Командныйпроект,написанныйдляучастия
- WEB1:taller1
- eloquent-ci:口才的ORM在CodeIgniter中的实现
- parcel-boilerplate:包裹2样板
- 商场营业员工作总结范文
- Panda-Dev-Website
- dynamic_widget:一个后端驱动的UI工具包,使用json构建动态UI,而json格式与flutter小部件代码非常相似