信号与系统分析：零极点图与系统稳定性

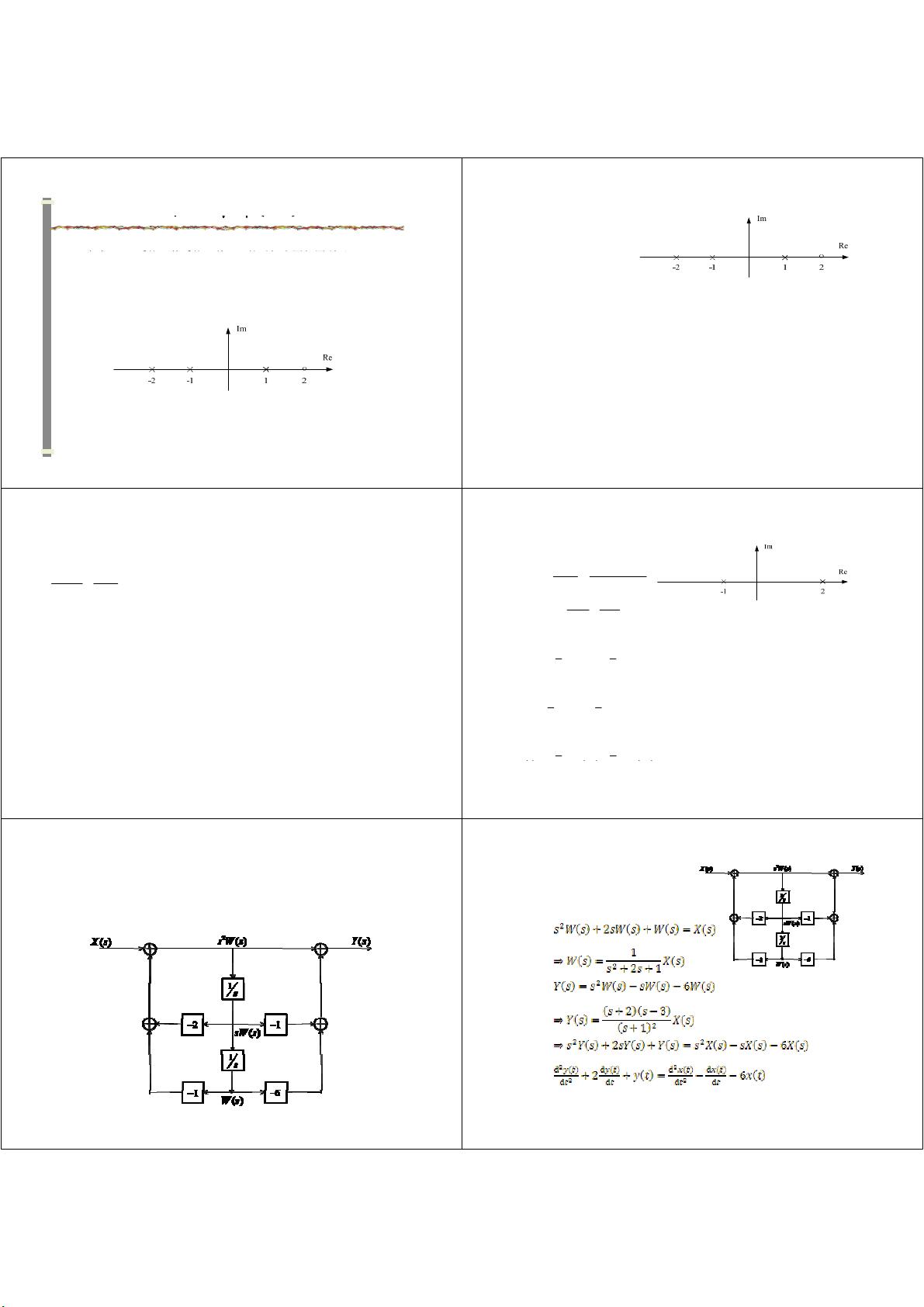
“信号与系统课程讲义，包含lec16_10.5-10.9的内容，涉及信号与系统的零极点图分析、稳定性判据和因果性判断，以及连续时间系统的微分方程解析。” 在信号与系统课程中，零极点图是分析线性时不变（LTI）系统特性的重要工具。该讲义中提到了一个LTI系统的零极点图，并要求根据图示分析相关的系统特性。零极点图是由系统函数H(s)的零点和极点在复平面上的分布构成，其中零点是H(s)的分母为零的点，极点是H(s)的分子为零的点。 题目中给出了四种可能的零极点配置，并要求判断与这些配置相关的系统是否稳定和因果。稳定性判据通常基于赫尔维茨稳定性条件，即所有极点必须位于s平面的左半部分。而因果性则要求系统函数的收敛域ROC（Region of Convergence）包含虚轴，即所有极点必须在虚轴的左侧。对于每种配置，分析如下： 1. 零点配置为{1}，极点配置为{-2, -3}。这种情况下，系统是稳定的，因为所有极点都在左半平面。同时，由于ROC包含虚轴，系统也是因果的。 2. 零点配置为{2, 1}，极点配置为{-1}。这个系统不稳定，因为有一个极点在右半平面。同时，由于ROC也包含了右半平面，系统是非因果的。 3. 零点配置为{1}，极点配置为{-1, -2}。系统是稳定的，但不是因果的，因为虽然所有极点都在左半平面，但ROC不包含虚轴。 4. 零点配置为∅（空集），极点配置为{-1}。系统是稳定的且因果的，因为极点都在左半平面，且ROC包含虚轴。 接下来，讲义中还涉及了一个连续时间系统的微分方程问题，其中输入信号x(t)和输出信号y(t)之间的关系通过微分方程表示。拉普拉斯变换被用来求解这个系统，其中H(s)是系统的传递函数，h(t)是系统的单位阶跃响应。 对于给定的微分方程，可以解出H(s)的表达式，并进一步确定零极点位置。这里H(s)被表示为两个多项式的比，即H(s) = (s^2 + 1)/(s^3 - s)，然后绘制零极点图。 根据这个传递函数，我们可以找到零点和极点的位置：零点为(-1, j, -j)，极点为(0, 1, -1)。系统是稳定的，因为所有极点都在左半平面。关于因果性，由于极点0位于虚轴上，ROC必须不包括实轴上的这段，所以系统是非因果的。 对于题目中的三种情况，分别求解了系统的单位阶跃响应h(t)的拉普拉斯逆变换，以验证系统的稳定性和因果性： 1. 当系统稳定且因果时，h(t)的ROC为Re[s] > -1，对应的h(t)为e^(-t)u(t)，其中u(t)是单位阶跃函数。 2. 当系统不稳定但非因果时，h(t)的ROC为Re[s] < -1，对应的h(t)为e^(2t)e^(-t)u(-t)。 3. 当系统稳定但非因果时，h(t)的ROC为Re[s] < 0，对应的h(t)为e^(t)e^(-t)u(-t)。 以上内容涵盖了信号与系统课程中的关键概念，包括零极点图分析、稳定性判据、因果性判断，以及连续时间系统微分方程的拉普拉斯变换解法。通过这些知识，学生可以理解和分析不同系统的行为特性。