不确定信息处理方法：敏感度分析与随机优化策略

处理不确定信息是许多实际问题中的关键挑战，特别是在资源分配、投资决策和优化领域。本文主要介绍了几种常见的方法来应对不确定性，包括敏感度分析、随机优化和稳定优化。 1. **敏感度分析** (Sensibility Analyze, Post-occupation)：这种方法首先假设不确定性可以用确定的参数表示，通过求解最优解，然后分析在最优解保持不变的前提下，参数变动范围内的效果。它适用于那些允许一定程度参数变化的情况，例如工程设计或投资组合优化，需考虑不同参数组合对结果的影响。 2. **随机优化** (Stochastic Optimization, Post-occupation)：基于历史数据，随机优化方法估计不确定参数的概率分布，然后寻找在可能的值区间内的最优解。这种做法适用于依赖随机变量的决策，如金融风险管理和供应链管理，需要预测不同可能情景下的最优策略。 3. **稳定优化** (Robust Optimization, Pre-occupation)：与前两者不同，稳定优化在决策制定阶段就考虑到不确定性。它通过构建一系列随机生成的方案，寻找在所有可能情况下的最稳健解决方案，适合于对极端情况有保护需求的场景，如军事战略规划。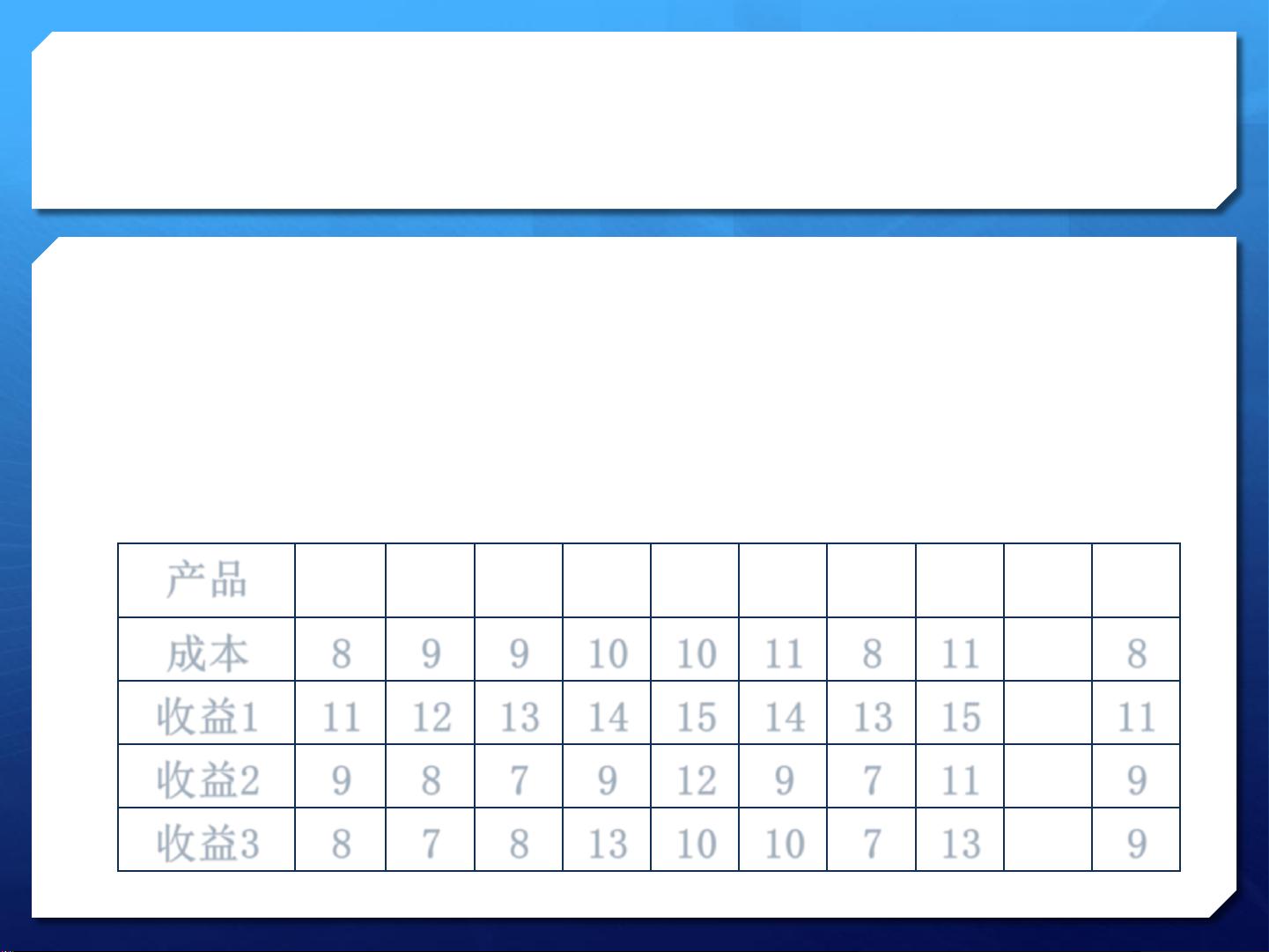 文章的核心部分聚焦于**稳定背包问题** (Absolute Robustness - Max-min Knapsack Problem, MNK)，这是一个经典的优化问题，最早由Jacobsen S.教授在1971年和Kaplan S.教授在1974年分别针对整数和实数情况提出。在该问题中，有n个投资产品，每个产品的收益存在不确定性。目标是找到一个投资组合，使得即使在最差的收益情况下，投资组合的总收益也尽可能大，同时控制投资成本不超过预算。 具体来说，稳定背包问题的数学模型可以表述为线性规划形式，涉及产品集𝐼，方案集𝑆，产品估值𝑣𝑖𝑠, 成本𝑤𝑖以及预算上限𝐶。问题的目标是找到一组决策变量𝑥𝑖（代表是否投资相应产品），使得在所有可能的收益方案下，投资组合的最小收益最大，并且满足成本限制。当观测方案数为1时，MNK简化为0-1背包问题。 总结来说，处理不确定信息的方法包括对参数敏感度的分析、概率分布驱动的随机优化以及直接面对不确定性的稳定优化策略。其中，稳定背包问题作为一种经典实例，展示了如何在面对复杂不确定性时寻求最稳健的决策方案。理解并应用这些方法对于解决现实世界中的优化问题具有重要意义。