Hankel-SVD滤波器：单集合基于特征处理的色流成像方法
需积分: 9 33 浏览量
更新于2024-09-08
收藏 2.43MB PDF 举报
"本文主要探讨了空时慢跳频抗干扰技术在超声成像中的应用，特别是通过一种称为Hankel-SVD滤波器的新型 eigen-处理方法来改善彩色血流图像的流动检测性能。该技术利用适应慢时间信号内容的特性，通过保留高于估算的杂波特征空间维度的主要成分，实现对杂波的抑制。"
在通信领域，尤其是军事通信和无线通信中，空时慢跳频（Space-Time Slow Frequency Hopping，STSFH）抗干扰技术是一种重要的信号处理策略。这种技术结合了空间分集和频率分集的优点，通过在时间和频率上随机变化通信频道，增加信号的抗干扰性和安全性。空时慢跳频技术的关键在于选择合适的跳频模式和速率，以确保在对抗有源干扰和无源干扰的同时，保持通信的效率和可靠性。
描述中提到的Hankel-SVD滤波器是针对超声成像中的颜色血流成像（Color Flow Imaging, CFI）提出的。超声成像是一种无创的医学诊断技术，用于实时观察人体内部器官和血管的血流状态。然而，超声成像受到多种因素的干扰，如组织运动、噪声以及回声信号中的杂波，这会影响流动检测的准确性。
Hankel矩阵是具有特定结构的矩阵，其每条对角线上的元素相同。在信号处理中，Hankel矩阵常用于分析信号的平稳性。Singular Value Decomposition (SVD) 是矩阵分解的一种方法，能够揭示矩阵的主成分。将两者结合，Hankel-SVD滤波器通过计算Hankel矩阵的SVD，可以识别并保留信号的主要特征，同时去除与杂波相关的低阶成分。
文章指出，Hankel-SVD滤波器首先应用于模拟的慢时间数据（ensemble size: 10），这些数据由两种不同流量参数集模拟得出，分别模拟动脉成像（血液速度：0到38.5cm/s，组织运动：最多2mm/s，发射频率：5MHz）。通过对模拟数据的处理，验证了Hankel-SVD滤波器在抑制杂波、提高血流检测性能方面的有效性。
这篇论文深入研究了空时慢跳频技术如何与超声成像的信号处理相结合，特别是在杂波抑制方面的新方法——Hankel-SVD滤波器。这种方法对于改善超声成像的质量，尤其是在复杂环境下（如快速移动的组织或高噪声环境）的血流成像，具有潜在的应用价值。
yu and cobbold: eigen-processing methods for color flow imaging—part i 561
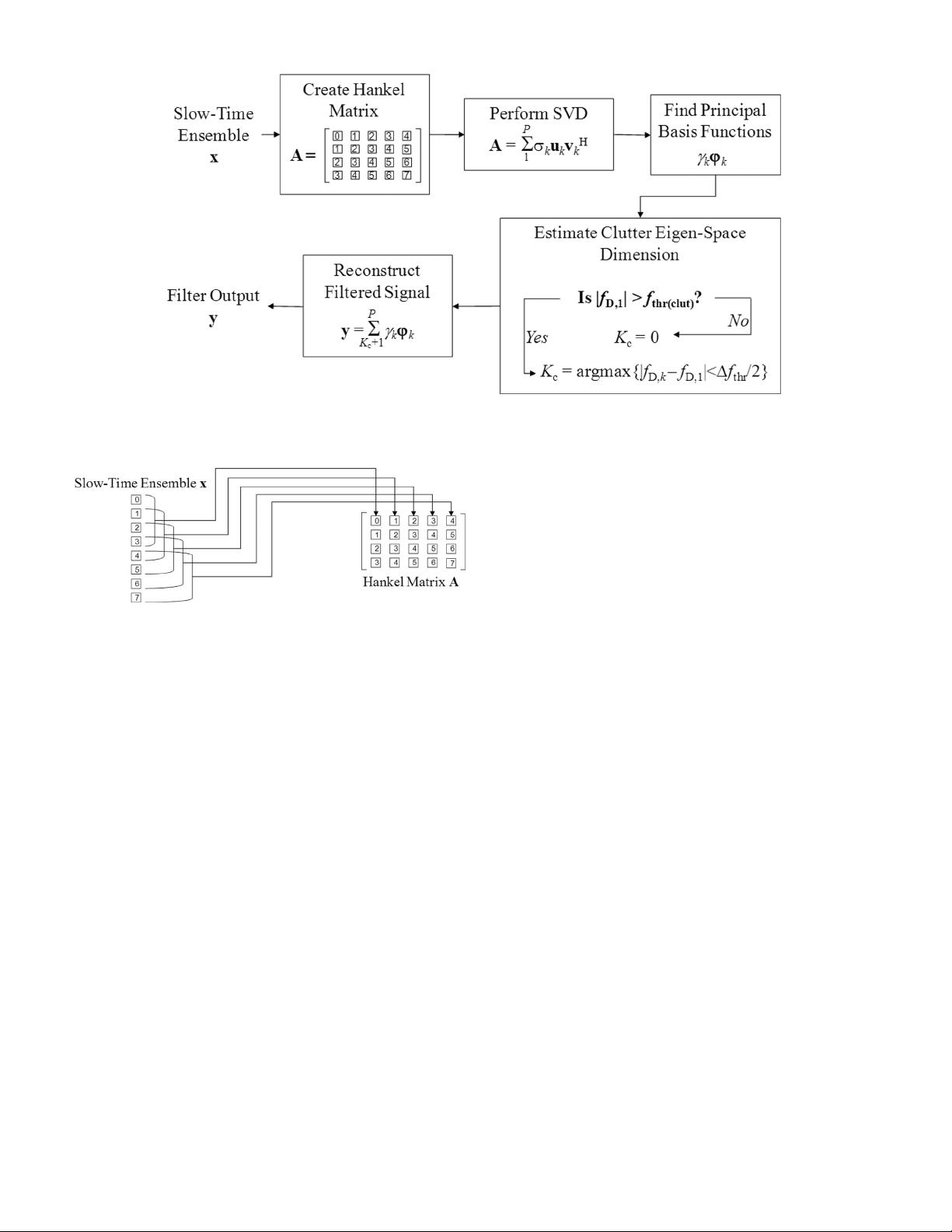
Fig. 1. Flow diagram of the proposed Hankel-SVD filter. During operation, the filter is applied to the slow-time ensemble of each sample
volume.
Fig. 2. Illustration of how the Hankel matrix A is constructed for
the case where the slow-time ensemble size is eight (N
D
=8)and
the dimension parameters is four (P =4).
where P must satisfy the relation P ≤ ceil(N
D
/2), i.e., the
smallest integer greater than or equal to N
D
/2. As such,
the relation P ≤ N
D
− P + 1 always holds, and the matrix
A has a rank (i.e., the number of independent rows) that is
equal to P with a largest possible rank of ceil(N
D
/2). An
example of the entire matrix formation process is shown in
Fig. 2. Note that, for this matrix, statistical stationarity
of the samples in the signal vector is inherently assumed.
To compute the P orthogonal components in the Hankel
component approximation, we can factor the Hankel data
matrix into the following sum of P orthogonal, rank-one
matrix components via the SVD:
A =
P
k=1
A
k
=
P
k=1
σ
k
u
k
v
H
k
. (3)
In this expression, A
k
is the kth rank-one Hankel compo-
nent in the decomposition, while σ
k
, u
k
,andv
k
are cor-
respondingly the singular value, left singular vector (with
dimension P ), and right singular vector (with dimension
N
D
− P +1) of A
k
. Note that the P singular values in
(3) are ordered from largest to smallest by definition, and
hence A
k
can be considered as the kth-order principal
Hankel component. From these principal Hankel compo-
nents, it is possible to reconstruct the orthogonal basis
vectors γ
k
ϕ
k
as seen in (1a). One particular way to per-
form this reconstruction process, as originally described
by Poon et al. [12], is to sum and average the matrix
elements along the reverse diagonals of A
k
because the
matrix more or less maintains a constant reverse-diagonal
structure. Such an approach is used by the proposed fil-
tering method.
B. Estimation of Clutter Eigen-Space Dimension
Because the aim of the Hankel-SVD filter is to suppress
clutter in the slow-time signal, it is necessary to determine
whether a principal Hankel component A
k
is part of the
clutter eigen-space. In general, there are two types of ap-
proaches to carry out this analysis. First, given that clut-
ter often has higher energy than blood echoes and white
noise, a principal Hankel component can be considered as
being part of the clutter eigen-space if its singular value
magnitude σ
k
is larger than a given value. Such way of
estimating the clutter eigen-space dimension is similar to
the eigenvalue analysis algorithms reported previously in a
few eigen-filter designs [7], [13]. Alternatively, since clutter
generally consists of low-frequency contents, it is possible
to identify a clutter eigen-space component based on the
frequency contents of each orthonormal basis vector ϕ
k
.
This latter approach is adopted in the Hankel-SVD filter
to determine the clutter eigen-space dimension because the
approach can be implemented in a way that gives filtering
characteristics similar to the stopband of a conventional
bandpass filter.
The clutter eigen-space analysis algorithm used by the
Hankel-SVD filter is illustrated in Fig. 3. This algorithm
is fundamentally based on two assumptions: 1) the slow-
time clutter is contained in the more dominant Hankel
components (i.e., ones with larger singular values); 2) the
blood flow component of the slow-time signal is contained
in the Hankel components with high Doppler frequen-
剩余13页未读，继续阅读
点击了解资源详情
点击了解资源详情
点击了解资源详情
2022-06-07 上传
2021-11-02 上传
2012-10-22 上传
点击了解资源详情
点击了解资源详情
点击了解资源详情
