线性代数习题集含答案解析,考研考试必备
需积分: 10 62 浏览量
更新于2024-07-18
1
收藏 1.35MB DOC 举报
"线性代数习题含答案,适合考研和考试复习,内容涵盖填空题、选择题、证明题、计算逆序数以及确定行列式符号和计算行列式值等核心知识点。"
线性代数是数学的一个基础分支,对于理解和解决许多科学和工程问题至关重要。本习题集主要涉及以下知识点:
1. 行列式的计算:行列式的值可以通过展开法则(如按行或按列展开)来计算。题目中出现了二阶和三阶行列式的计算,这些都是基础中的基础,对于理解行列式的性质至关重要。例如,题目中给出的二阶行列式的答案揭示了行列式与矩阵元素之间的关系。
2. 行列式的性质:在证明题中,可能需要利用行列式的性质,比如将一个行列式“拆项”成其他行列式的和,以求得证明。这种技巧经常用于简化复杂问题。
3. 逆序数与排列的奇偶性:逆序数用于确定排列的奇偶性,是组合数学中的一个重要概念。题目中通过计算逆序数来判断9级排列的奇偶性,这有助于理解拉普拉斯展开和行(列)互换对行列式的影响。
4. 选择题:选择题考察了行列式等于零的条件、行列式中的变量解、行列式的值等问题,这些都是线性代数的基础知识,对于解决更复杂的问题(如线性方程组的求解)至关重要。
5. 行列式符号的确定:题目要求确定六阶行列式中特定项的符号,这涉及到行列式的交替性质,即行列式中每交换两行(列)的顺序,其值会乘以-1。
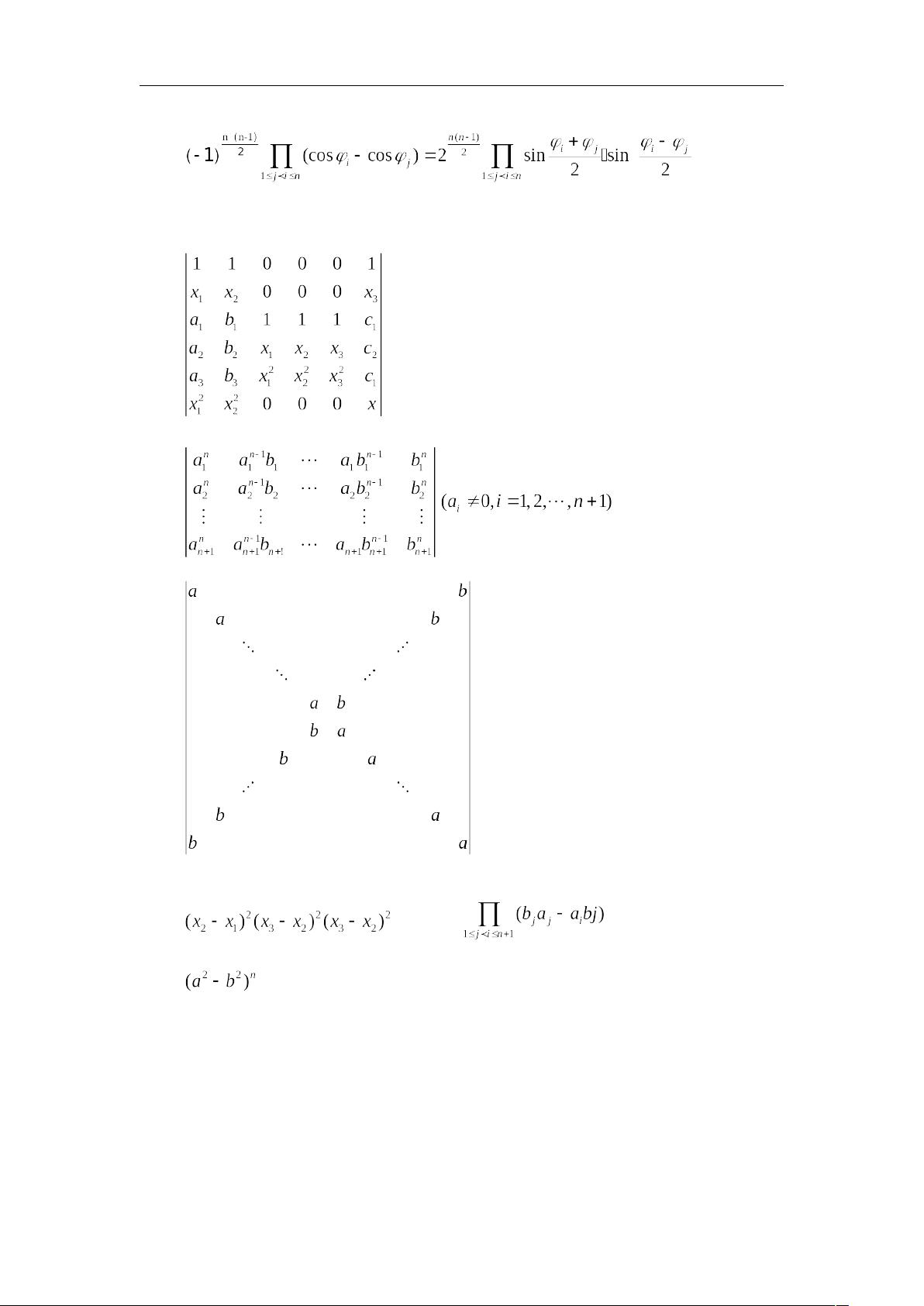
6. 计算行列式的值:题目给出了多个行列式的值计算,包括简单的数值行列式和含有变量的行列式,这些练习旨在强化对行列式计算规则的理解。
7. 应用:线性代数在考研和考试中常常涉及到实际应用,例如在计算逆序数时,可以联想到它在计算机科学中的应用,如排序算法的分析。
通过解答这些习题,学生能够巩固线性代数的基本概念,提高解决问题的能力,并为未来的考研或考试做好充分准备。在学习过程中,不仅要掌握公式和计算方法,更要理解每个概念背后的数学原理,这样才能真正驾驭线性代数这一强大的数学工具。
2009-02-26 上传
2021-10-03 上传
2022-01-05 上传
2013-06-02 上传
2010-04-20 上传
2022-08-08 上传
olongingfor
- 粉丝: 0
- 资源: 6
最新资源
- 黑板风格计算机毕业答辩PPT模板下载
- CodeSandbox实现ListView快速创建指南
- Node.js脚本实现WXR文件到Postgres数据库帖子导入
- 清新简约创意三角毕业论文答辩PPT模板
- DISCORD-JS-CRUD:提升 Discord 机器人开发体验
- Node.js v4.3.2版本Linux ARM64平台运行时环境发布
- SQLight:C++11编写的轻量级MySQL客户端
- 计算机专业毕业论文答辩PPT模板
- Wireshark网络抓包工具的使用与数据包解析
- Wild Match Map: JavaScript中实现通配符映射与事件绑定
- 毕业答辩利器:蝶恋花毕业设计PPT模板
- Node.js深度解析:高性能Web服务器与实时应用构建
- 掌握深度图技术:游戏开发中的绚丽应用案例
- Dart语言的HTTP扩展包功能详解
- MoonMaker: 投资组合加固神器,助力$GME投资者登月
- 计算机毕业设计答辩PPT模板下载