Matlab实现线性回归：从单变量到多变量及正规方程

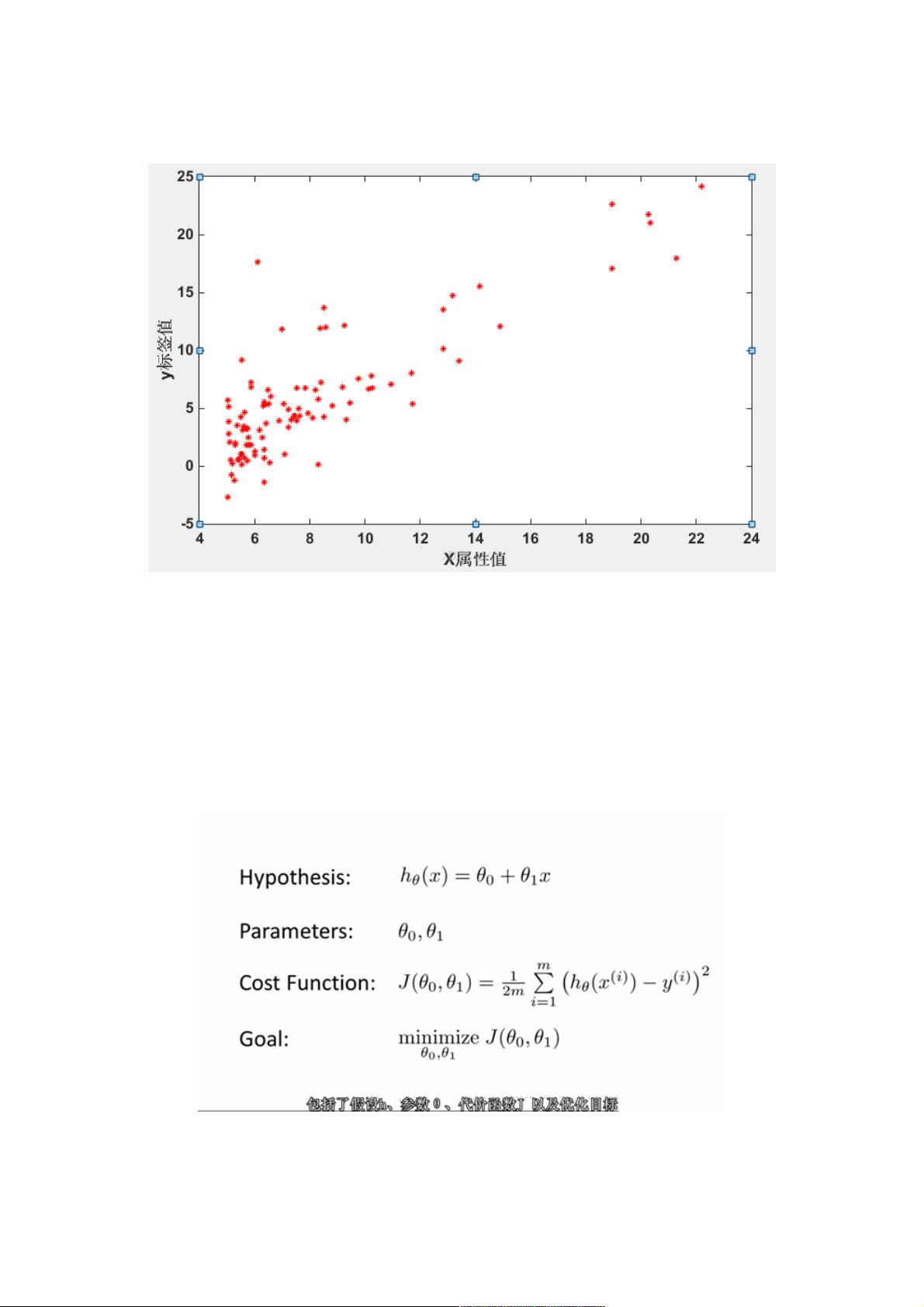
"线性回归是一种广泛应用的统计学方法，用于建立因变量与一个或多个自变量之间的线性关系。在本资源中，我们将探讨如何在Matlab环境下实现线性回归算法，包括单变量和多变量的情况，并比较了梯度下降法和正规方程两种求解方法。" 线性回归算法在机器学习领域中扮演着基础且重要的角色，它假设因变量与自变量之间存在线性关系。在Matlab实现中，通常涉及以下几个步骤： 1. **设定线性函数**（Hypothesis）：线性回归模型可以表示为`hθ(x) = θ0 + θ1 * x1`，其中`hθ(x)`是预测值，`θ0`和`θ1`是模型参数，`x1`是自变量。对于单变量问题，只有一个自变量`x1`；而对于多变量问题，会有多个自变量，如`x1, x2, ..., xn`，此时模型变为`hθ(x) = θ0 + θ1 * x1 + θ2 * x2 + ... + θn * xn`。 2. **选择损失函数**（Cost Function）：通常选用均方误差（Mean Squared Error, MSE）作为损失函数，表示为`J(θ) = (1/(2m)) * ∑(hθ(xi) - yi)^2`，其中`m`是样本数量，`yi`是实际的标签值。 3. **优化方法**：有两种常见的优化策略： - **梯度下降法**（Gradient Descent）：通过不断迭代更新参数`θ`来最小化损失函数`J(θ)`。在每次迭代中，`θ`会朝着损失函数下降最快的方向调整。对于线性回归，更新规则为`θj := θj - α * (1/m) * ∑(hθ(xi) - yi) * xi_j`，其中`α`是学习率，`xi_j`是第`i`个样本的第`j`个特征值。 - **正规方程**（Normal Equation）：通过求解`X^T * X * θ = X^T * y`来直接获得最佳的`θ`值，其中`X`是特征矩阵，`y`是目标向量。这种方法在特征数较少时效率较高。 在Matlab中，实现线性回归可以编写相应的函数来计算损失函数、梯度以及进行参数更新。对于多变量线性回归，只需扩展自变量的数量并相应地修改损失函数和梯度下降的更新规则。 在实际应用中，我们还需要注意数据预处理，包括数据清洗、标准化等步骤，以确保模型的稳定性和准确性。同时，评估模型性能通常会使用如R²分数、均方根误差（RMSE）等指标。 总结来说，线性回归是预测分析的基础工具，通过Matlab实现，可以方便地处理单变量和多变量的问题。梯度下降和正规方程是两种常见的参数求解方法，各有适用的场景。在实践中，根据数据规模和计算资源，选择合适的方法是至关重要的。