Analog Applications Journal
High-Performance Analog Products www.ti.com/aaj 3Q 2012
Texas Instruments Incorporated
8
Designing a Qi-compliant receiver coil
for wireless power systems, Part 1
Overview
The implementation of the Wireless Power Consortium’s
(WPC’s) Qi standard
1
brings wireless power to many dif-
ferent end applications. The receiver (Rx) coil for each
application may have different geometries and/or power
requirements. Since the Rx coil is a key component in a
successful and efficient design of a Qi-compliant Rx and
there are many design options and trade-offs to consider,
the designer must take a careful and methodical approach
when realizing a solution. This article provides the techni-
cal insight needed to realize a successful Rx-coil design. It
covers the Qi-compliant system model as a basic trans-
former; Rx-coil measurements and system-level influ-
ences; and methods of qualifying a design for successful
operation. It is assumed that the reader has a general
understanding of the Qi-compliant inductive power sys-
tem. Background information can be found in Reference 2.
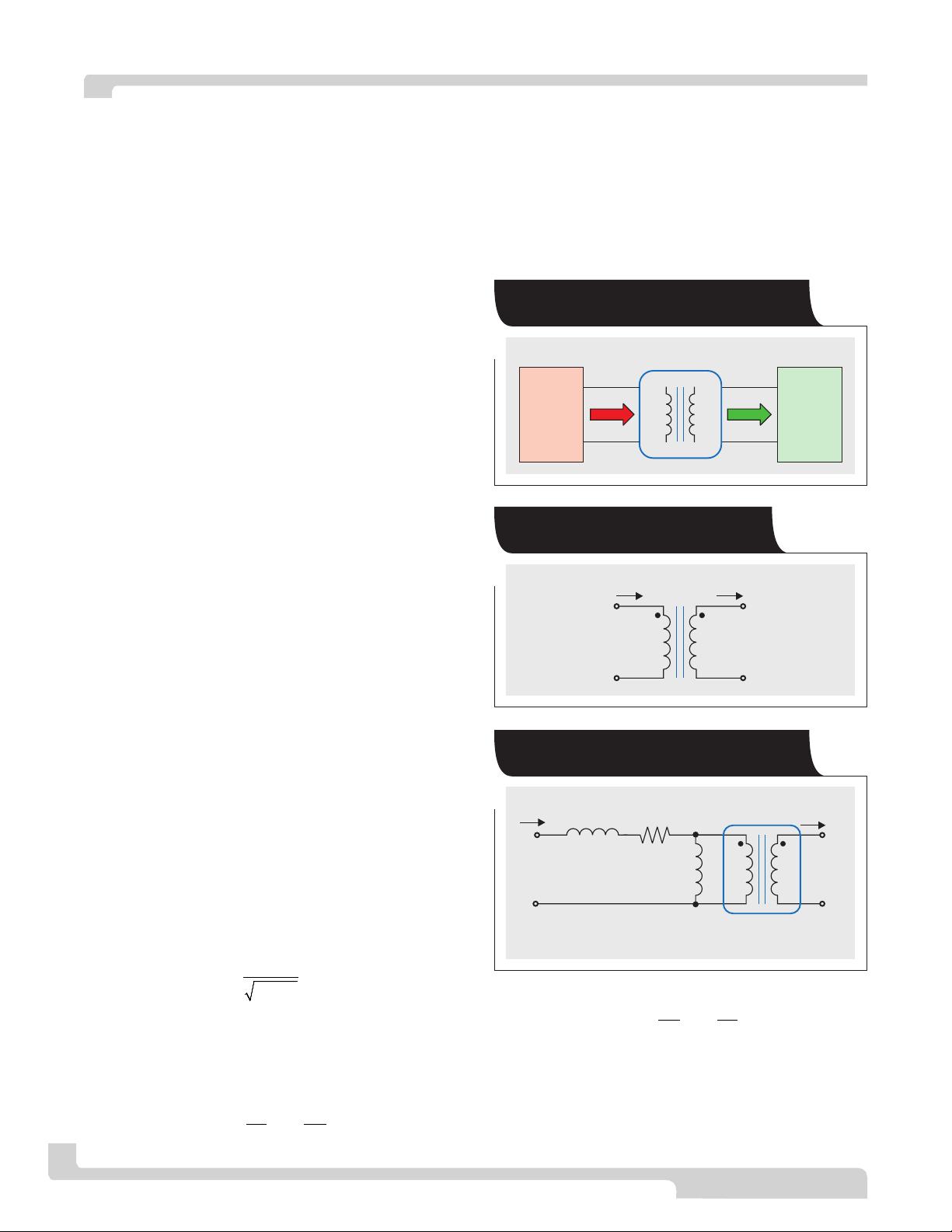
Qi-compliant system as a transformer
For many near-field wireless power systems such as the
one specified by the WPC, the behavior of the magnetic
power transfer can be modeled by a simple transformer. A
traditional transformer usually has a single physical struc-
ture with two windings around a core material that is
highly permeable compared to air (Figure 1). Since the
traditional transformer uses a highly permeable material to
carry the magnetic flux, most (not all) of the flux produced
by one coil couples to the second coil. This coupling, which
can be measured through a parameter known as the cou-
pling coefficient, is denoted as k (a measure that can have
a value between 0 and 1).
Three parameters define a two-coil transformer:
L
11
is the self-inductance of coil 1.
L
22
is the self-inductance of coil 2.
L
12
is the mutual inductance of coils 1 and 2.
The coefficient for coupling between the two coils can be
formulated as
12
11 22
L
k
L L
=
. (1)
The ideal transformer then can be modeled by using a
coupled inductor as shown in Figure 2.
Using the voltage and current relationship of an induc-
tor can provide the nodal equations of this two-coil
transformer:
1 2
1 11 12
di di
V L L
dt dt
= + (2a)
2 1
2 22 12
di di
V L L
dt dt
= + (2b)
For circuit analysis, the model in Figure 2 can be repre-
sented by what traditionally is referred to as a cantilever
model, shown in Figure 3. Here the magnetic coupling and
mutual inductance are simplified to leakage and magnetiz-
ing inductances. This allows the physical nature of the
By Bill Johns, Applications Engineer,
Tony Antonacci, System Engineer,
and Kalyan Siddabattula, System Engineer
Power Management
k >> 0.95
Send
Energy
Receive
Energy
Figure 1. Traditional transformer with one
physical structure
V
1
V
2
i
1
i
2
+
+
–
–
Figure 2. Ideal model of a traditional
transformer
1:N
e
Ideal
Transformer
L
Leak
L
Mag
V
1
V
2
i
1
i
2
+
+
–
–
Figure 3. Cantilever model of a traditional
transformer









