"深入理解堆：完全二叉树结构与应用"

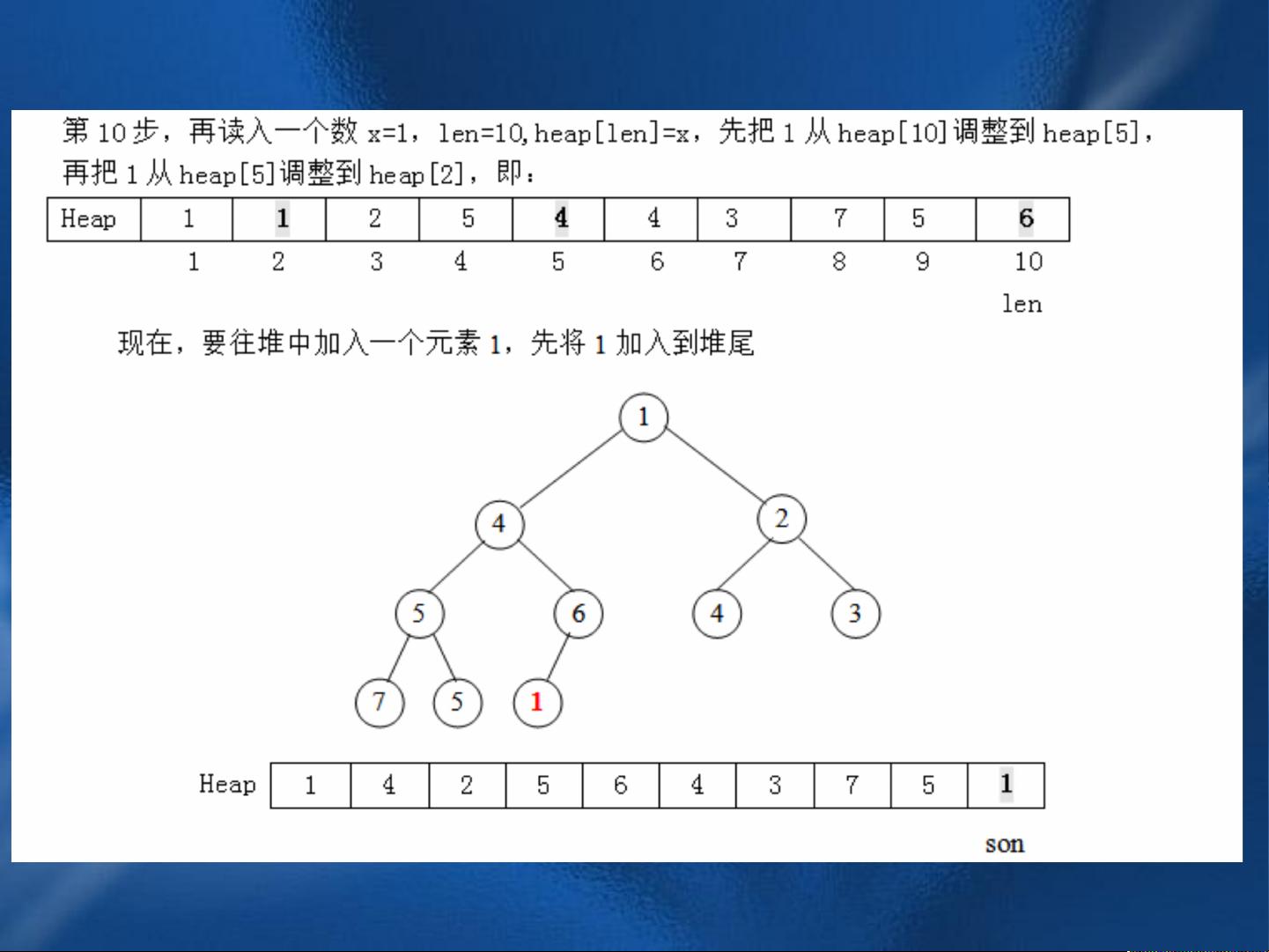
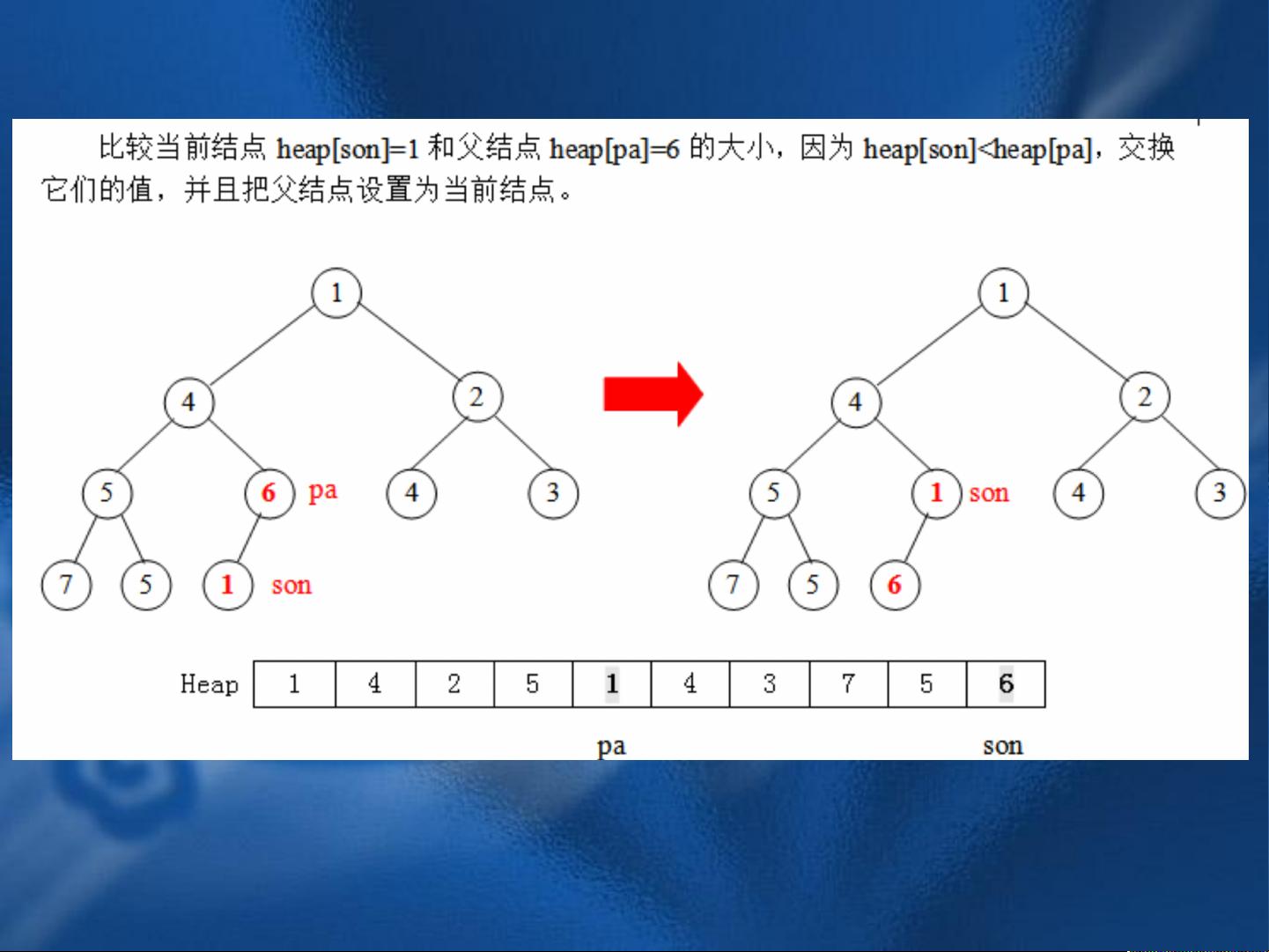
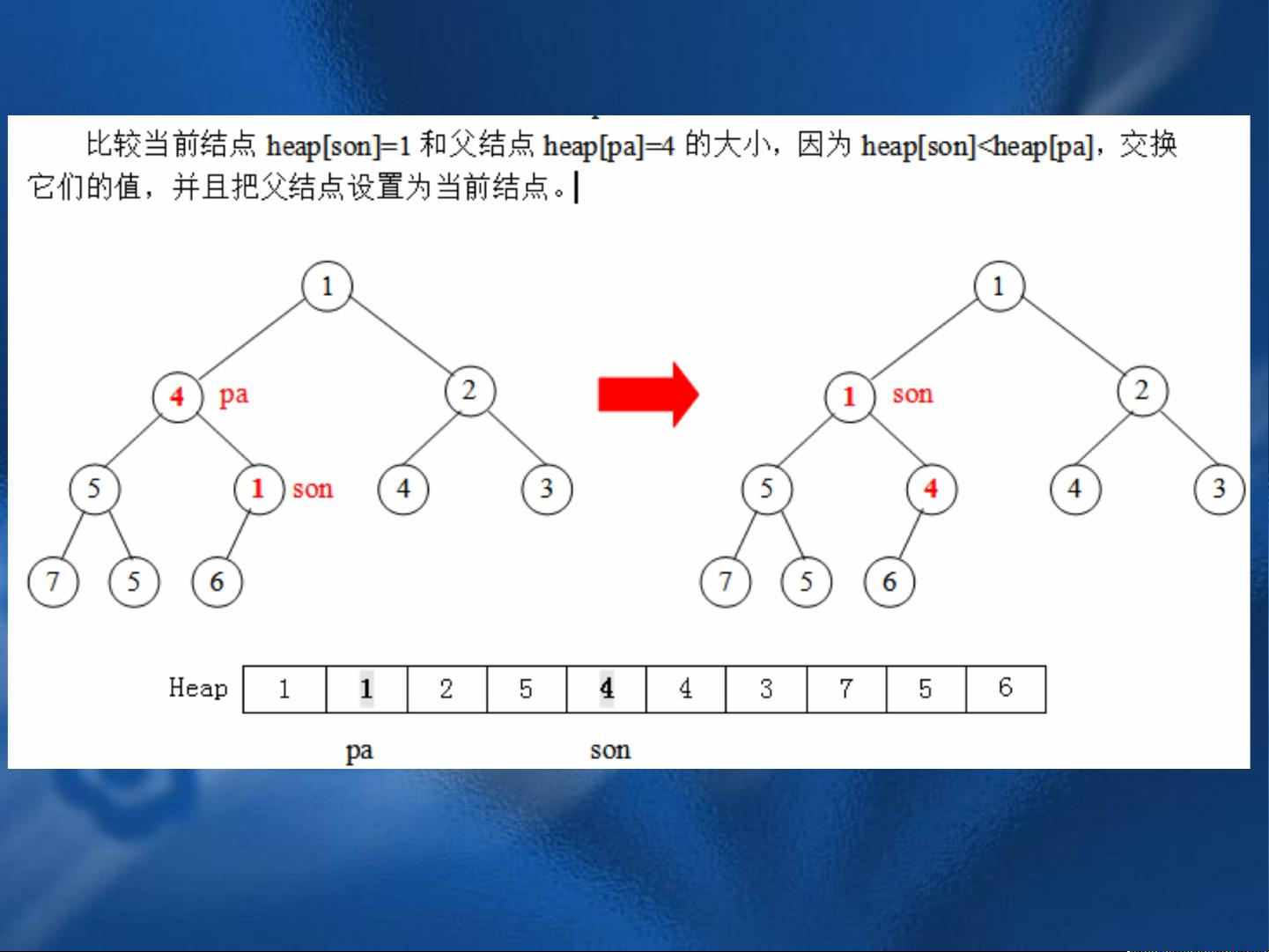
第三章第三节讲述了堆及其应用。在预备知识部分，介绍了完全二叉树的概念，即只有最下面一层的结点数小于2i-1，并且都集中在最左边的若干位置。堆的定义是一种数组对象，可以被视为一棵完全二叉树。每个结点与数组中存放该结点中值的元素相对应。堆的性质包括数组A的长度为len，二叉树的结点个数为size，size≤len，并且能够方便地求出每个结点的父结点、左孩子结点、右孩子结点的下标。最重要的是，堆具有结点值不得超过其父结点值的性质，即最大元素存放在根结点中。这些性质使得堆在实际应用中具有重要意义。 堆在计算机科学中有着广泛的应用，其中最常见的是堆排序算法。堆排序是一种时间复杂度为O(nlogn)的排序算法，思路是先构建一个最大堆（根结点值最大），然后将堆顶元素与最后一个元素交换，并重新调整堆，再取出堆顶元素，如此循环直至所有元素有序。堆排序的稳定性取决于堆的性质，因为堆中的元素并不是按照插入的顺序来排序的，所以排序结果不具有稳定性。 堆还可以用来解决一些实际问题，比如优先队列的实现。优先队列是一种特殊的队列，每次出队时都会返回队列中最高（最低）优先级的元素。基于堆的优先队列可以在O(logn)的时间内实现插入元素、删除元素和获取优先级最高元素等操作，这在很多算法问题中都有重要的应用。 除了堆排序和优先队列，堆还可以用来解决一些图论中的算法问题，比如最短路径算法中的Dijkstra算法和Prim算法。Dijkstra算法通过维护一个优先队列来不断更新到各个顶点的距离，而Prim算法通过维护一个最小生成树的集合来逐步构建最小生成树。这些算法的实现离不开堆的数据结构。 总的来说，堆是一种非常重要的数据结构，具有很多优秀的性质和应用。掌握堆的基本原理和操作将有助于更好地理解和应用相关算法和数据结构，提高编程能力和解决问题的效率。希望大家能够认真学习和理解堆及其应用，为自己的进步打下坚实的基础。