Python机器学习实战：逻辑回归的理论与优化

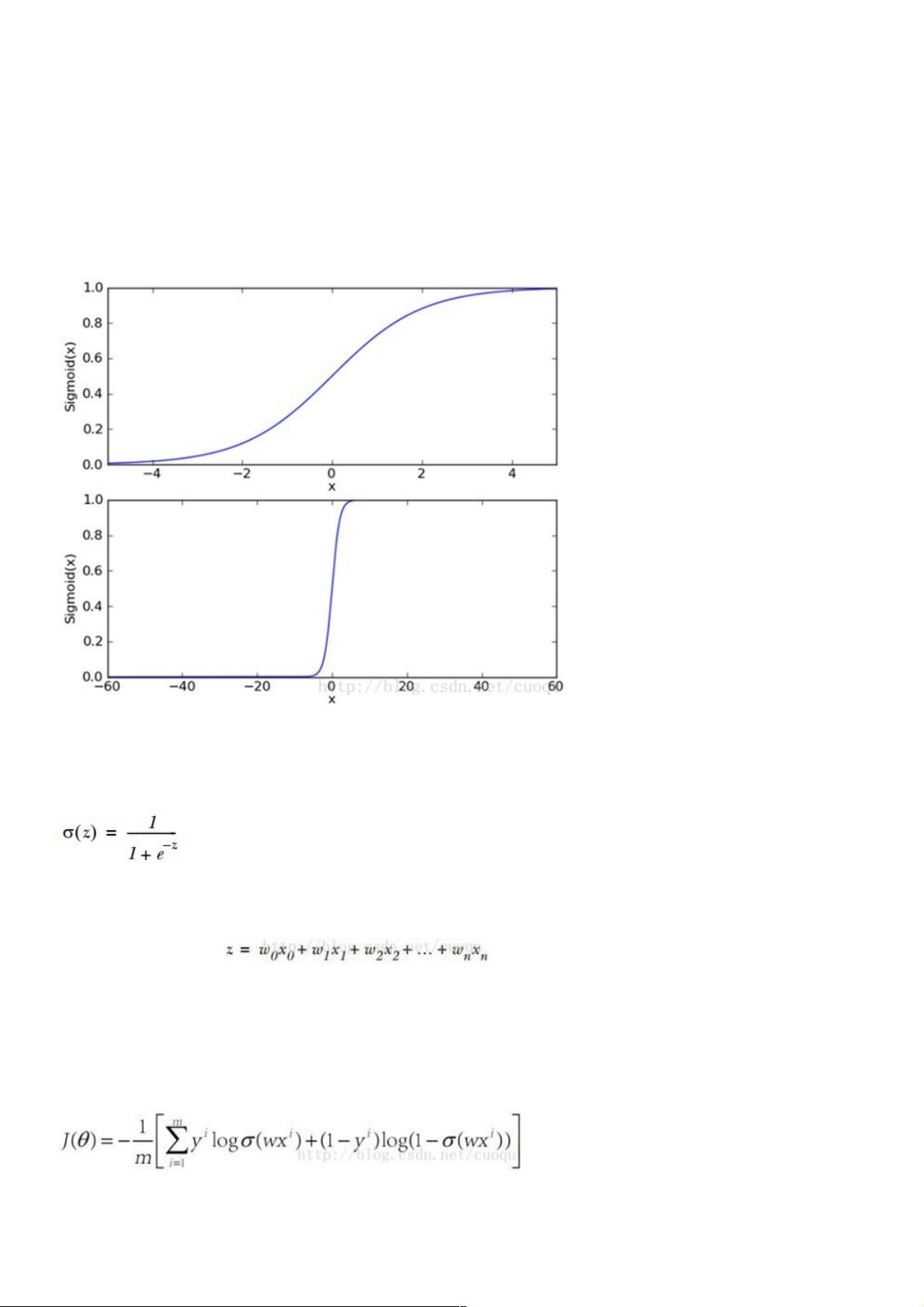
本篇内容深入探讨了Python机器学习中的逻辑回归理论与实战。在传统的机器学习流程中，逻辑回归标志着正式学习的开始，因为它涉及构建价值函数（cost function），通过优化找到权重，并进行测试验证。逻辑回归作为有监督学习方法，主要应用于预测和分类任务，不同于线性回归的简单线性关系，它采用非线性sigmoid函数进行拟合，该函数的连续性和可导性使其在优化过程中更为便利。 sigmoid函数（公式一）是逻辑回归的核心，它的形状决定了它适用于二类分类问题，由于其强烈的一级分化特性。为了将特征映射到sigmoid函数的输出，我们需要计算权重向量W，其中每个权重对应于输入特征的一个系数。通过大量的训练样本，目标是找到一组权重，使得输入特征经过加权后通过sigmoid函数产生的输出能够准确地对应于类别标签。 优化权重的过程通常使用梯度下降算法，这种方法寻找的是训练误差的最小化方向。梯度下降法包括常规梯度下降和随机梯度下降，它们通过计算损失函数关于权重的梯度，即函数在当前点上升最快的方向，然后沿着这个方向更新权重，逐步减小误差，直到达到局部最优解。虽然这有助于提高模型性能，但过度拟合的风险仍然存在，需要在实践中谨慎处理。 总结来说，本文介绍了逻辑回归的理论基础，包括sigmoid函数的选择、权重优化的梯度下降方法以及如何将特征映射到模型中进行预测。理解这些核心概念对于实际应用逻辑回归进行数据分析和预测至关重要。