C++ 动态规划解析：最长公共子序列（LCS）与递归策略

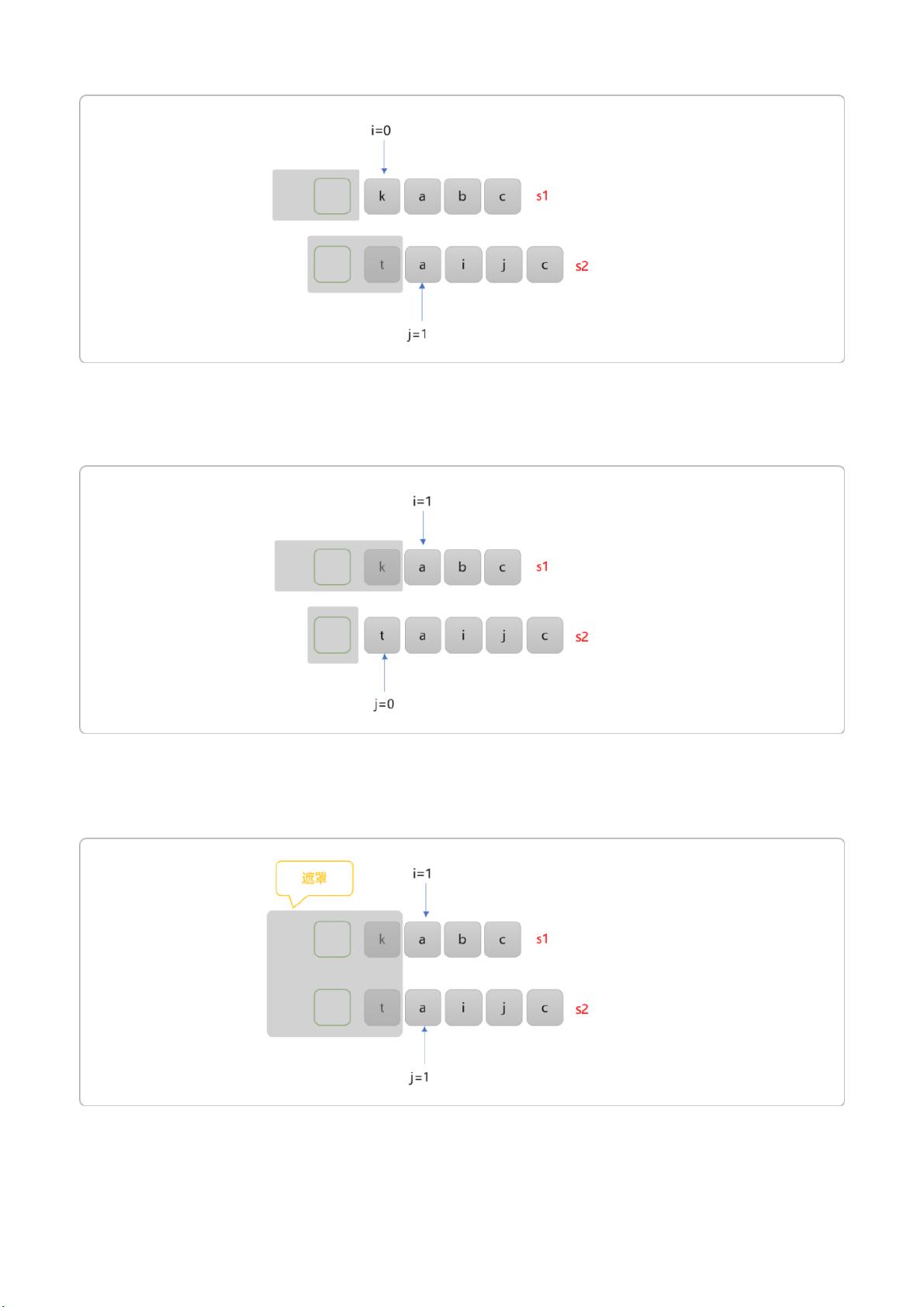
"这篇文档是关于C++实现动态规划解决最长公共子序列（LCS）问题的案例解析，探讨了递归与动态规划之间的关系。文档深入浅出地介绍了LCS问题及其解决策略，旨在帮助读者理解并掌握相关算法。 最长公共子序列(LCS)问题是一个经典的计算机科学问题，它涉及寻找两个或多个字符串之间的最长序列，这些序列不必连续但必须保持原有的相对顺序。例如，字符串's1=kabc'和's2=taijc'的LCS是'ac'。LCS问题常常被用来比较文本或生物序列的相似性。 在解决LCS问题时，递归思想是一个重要的起点。通过定义一个函数，如'intlcs(string s1, int i, string s2, int j)'，表示在s1的第i个字符和s2的第j个字符的位置开始计算LCS。当i和j都为0时，我们处理的是完整字符串的情况。若s1[i]不等于s2[j]，我们可以选择以下三种递归情况： 1. 不改变i，将j加1，即比较s1的子串从i开始和s2的子串从j+1开始的LCS。 2. 将i加1，不改变j，比较s1的子串从i+1开始和s2的子串从j开始的LCS。 3. 同时将i和j加1，比较s1的子串从i+1开始和s2的子串从j+1开始的LCS。 每个递归调用都会减小问题的规模，直到达到基本情况，即空字符串与空字符串的LCS显然是空字符串。然后，通过回溯这些递归调用，我们可以构建一个解决方案，通常使用动态规划来避免重复计算。 动态规划方法的核心是创建一个二维数组，如dp[i][j]，存储s1的前i个字符和s2的前j个字符的LCS长度。基本策略是根据字符是否匹配来填充这个数组： - 如果s1[i]等于s2[j]，那么dp[i][j]应该是dp[i-1][j-1]加上1，因为当前字符也包含在LCS中。 - 如果s1[i]不等于s2[j]，则dp[i][j]将是dp[i-1][j]、dp[i][j-1]和dp[i-1][j-1]中的最大值，这取决于上述三种选择中的哪一种能得到更长的子序列。 通过这种方式，我们可以自底向上地填充dp数组，并在最后一行的最后一列找到整个字符串的LCS长度。为了获取实际的LCS，我们可以从dp[s1.length()-1][s2.length()-1]开始，逆向跟踪dp数组中的路径。 总结来说，C++动态规划解决LCS问题涉及递归思想的转化和二维数组的填充，这不仅揭示了动态规划解决问题的本质，也为其他优化和复杂问题的解决提供了基础。理解和掌握这一算法对于提升编程技能和解决实际问题具有重要意义。"