计算机逻辑基础：半加器与全加器详解

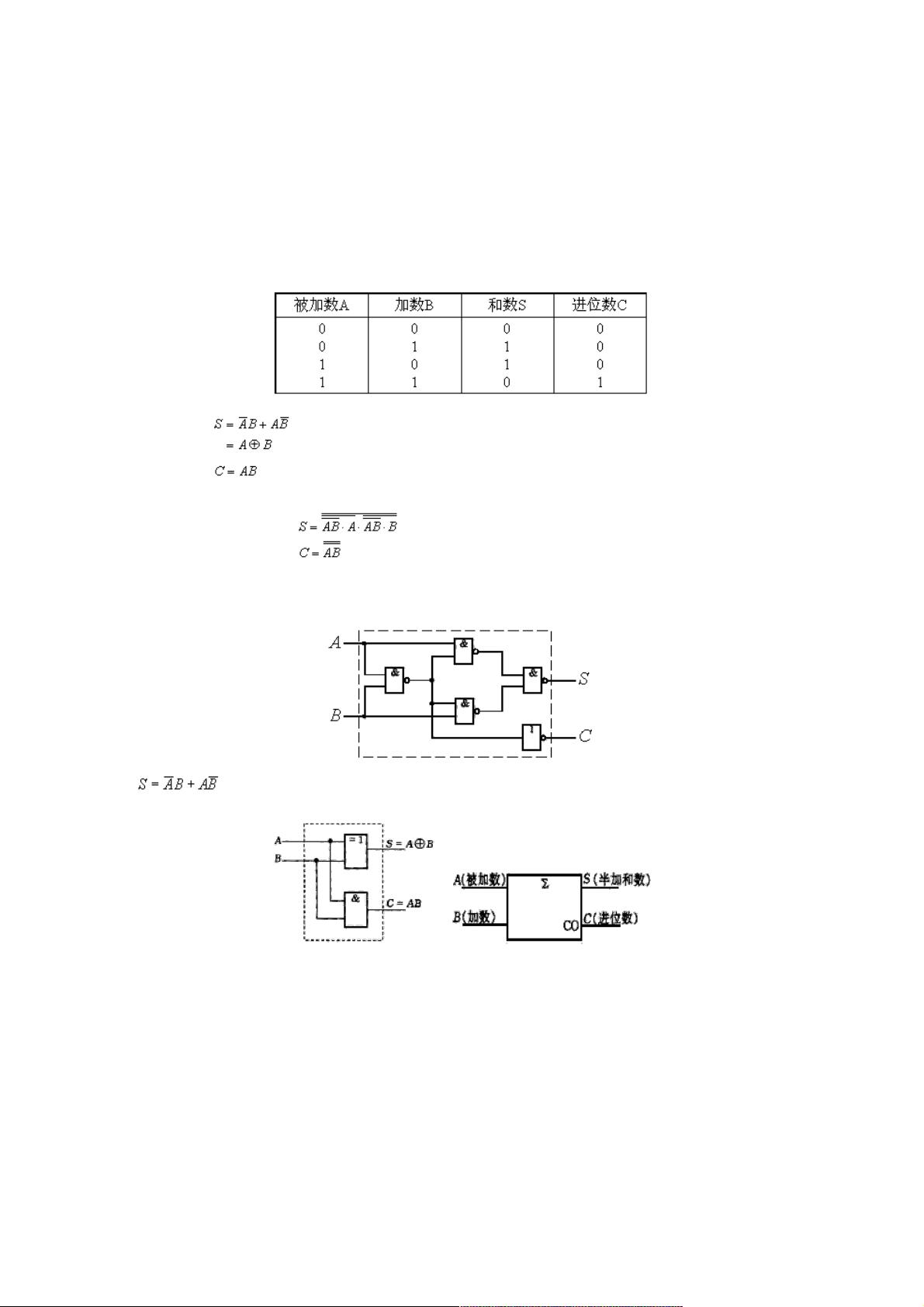
算术运算电路是数字系统的核心组成部分，它在计算机硬件中扮演着基础的角色，负责执行基本的数学运算。本节主要讨论的是加法和减法这两种关键运算的逻辑电路实现。 首先，我们从最基本的算术运算单元——半加器和全加器开始。半加器是用于单个二进制位相加的逻辑电路，它仅考虑两个输入的加数，忽略进位信号。半加器通过逻辑代数分析，可以利用与非门构造，其功能是计算两个输入的异或（XOR）和保持进位不变。半加器的符号表示了其异或和与保持功能。 全加器则更为复杂，它可以处理加数、被加数和来自低位的进位信号。全加器的真值表描述了这些输入如何映射到和数和新的进位。通过卡诺图化简，我们可以得到全加器的逻辑表达式，进而设计出由与非门构成的电路。全加器的符号直观展示了其加法和进位功能。 在处理多位数加法时，我们有两种策略：串行进位加法器和超前进位加法器。串行进位加法器采用逐位相加的方式，每个位的计算依赖于前一位的进位，速度较慢但结构简单。例如，使用集成电路如74LS283构建的四位串行进位加法器就是基于全加器的串联。 超前进位加法器则通过预先处理进位信号，使得每位的计算独立于低位，提高了运算速度。这种电路设计的关键在于定义中间变量，比如Gi和Pi，来控制进位的发生。通过全加器的逻辑表达式，我们可以构建出超前进位的逻辑电路，使得整个加法过程更为高效。 总结来说，算术运算电路涵盖了从基本的半加器和全加器设计到多位数加法器的不同实现策略，包括串行和超前进位。理解这些电路的工作原理对于深入研究数字逻辑设计和计算机硬件有着至关重要的作用。无论是嵌入式系统开发还是处理器内部的运算单元设计，掌握算术运算电路都是必不可少的技能。