"ACM算法与程序设计(六):最短路问题的解决和应用"
需积分: 0 56 浏览量
更新于2024-01-19
收藏 816KB PDF 举报
ACM算法与程序设计(六)最短路6. 最短路详细介绍了最短路径问题及其解决方法。最短路径问题可以分为单源最短路和多源最短路两种情况。单源最短路是指从一个起点出发求到其他所有顶点的最短路径,而多源最短路是指从多个起点出发求到其他所有顶点的最短路径。在单源最短路部分,课程着重介绍了Dijkstra算法及其应用——差分约束系统。
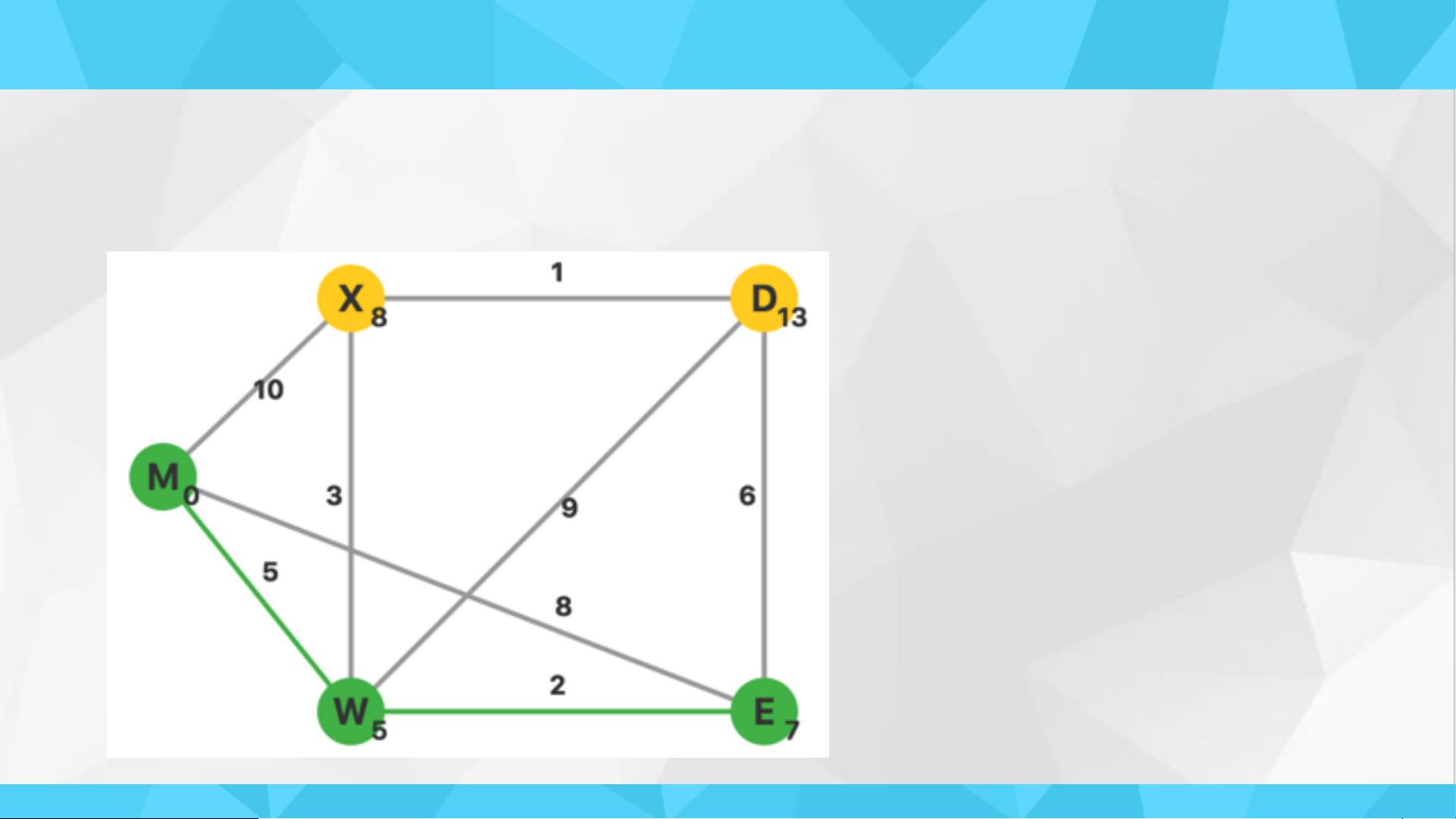
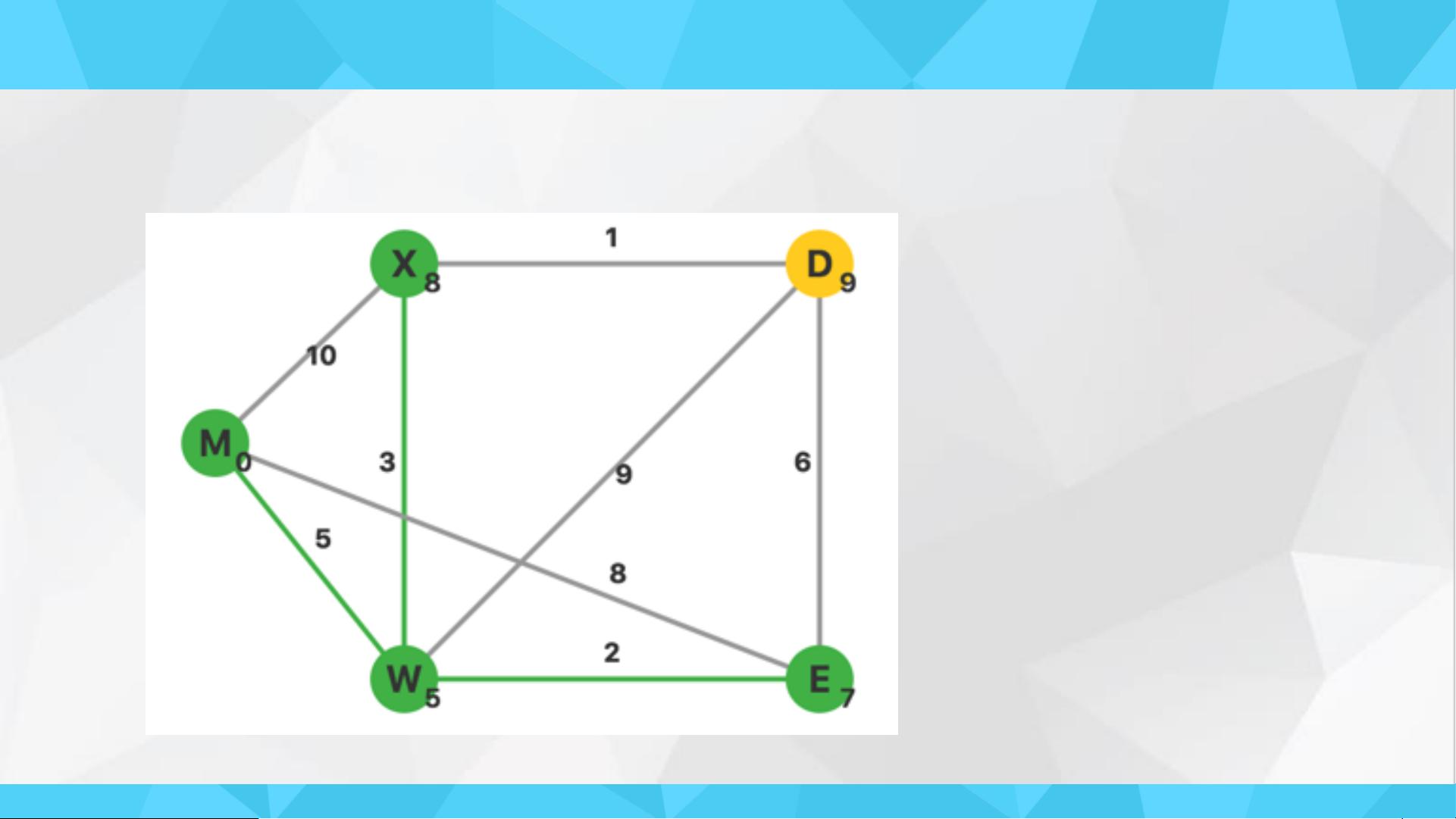
Dijkstra算法是一种常用的解决单源最短路径问题的算法,主要特点是以起点为中心,逐层向外扩展,每次都会选择一个最近点继续扩展,直到取完所有点。算法的前提是图中不能出现负权边,否则会导致计算出错。
算法的实现步骤如下:
1. 首先定义带权图G的顶点集合为V,将源点s加入已确定最短路径的顶点集合U,初始集合U为空。
2. 初始化源点s到每个顶点的距离dist为正无穷,源点s到自身的距离为0。
3. 逐步更新dist值,从集合V-U中选择一个距离源点最近的顶点v加入集合U。
4. 对于v的每个邻接顶点u,更新源点s到u的距离dist[u],如果经过v到u的距离更短,则更新dist[u]的值。
5. 重复第3、4步操作,直到集合V-U为空或无法找到从源点s出发到达其他顶点的路径。
Dijkstra算法的时间复杂度为O(V^2),其中V为图中的顶点数。为了提高算法的效率,在实际应用中可以使用优先队列来实现。通过维护每个顶点的最短距离值,优先队列可以快速找到距离源点最近的顶点,从而加快算法的执行速度。
除了Dijkstra算法,课程还介绍了另一种解决单源最短路径问题的算法——SPFA算法。SPFA算法是一种基于队列实现,用于求解带负边权的图的最短路径问题。与Dijkstra算法相比,SPFA算法的时间复杂度更优,可以达到O(VE),其中V为顶点数,E为边数。然而,SPFA算法对于存在负权环的情况下可能出现无限循环的问题,因此在实际使用中需要进行判断和优化。
另外,课程还介绍了解决多源最短路径问题的算法——Floyd算法。Floyd算法通过构建一个二维数组来记录任意两个顶点之间的最短路径,从而求解出整个图的最短路径问题。Floyd算法的时间复杂度为O(V^3),其中V为顶点数。
最后,课程还介绍了单源最短路径的一个经典应用——差分约束系统。差分约束系统是一种常见的数学模型,用于描述一组变量与变量之间的关系和限制。通过将差分约束系统转化为带权图,并利用Dijkstra算法求解最短路径,可以得到满足约束条件的变量取值。
总之,ACM算法与程序设计(六)的最短路部分详细介绍了最短路径问题及其解决方法。通过学习Dijkstra算法、SPFA算法、Floyd算法和差分约束系统的应用,可以有效地解决各种最短路径问题。这些算法在实际应用中具有重要的意义,可以用于路径规划、网络优化等领域。
2012-10-24 上传
2022-08-03 上传
2022-08-03 上传
2022-08-03 上传
2009-04-15 上传
2014-07-30 上传
2011-10-09 上传
2011-05-19 上传
whph
- 粉丝: 28
- 资源: 305
最新资源
- 黑板风格计算机毕业答辩PPT模板下载
- CodeSandbox实现ListView快速创建指南
- Node.js脚本实现WXR文件到Postgres数据库帖子导入
- 清新简约创意三角毕业论文答辩PPT模板
- DISCORD-JS-CRUD:提升 Discord 机器人开发体验
- Node.js v4.3.2版本Linux ARM64平台运行时环境发布
- SQLight:C++11编写的轻量级MySQL客户端
- 计算机专业毕业论文答辩PPT模板
- Wireshark网络抓包工具的使用与数据包解析
- Wild Match Map: JavaScript中实现通配符映射与事件绑定
- 毕业答辩利器:蝶恋花毕业设计PPT模板
- Node.js深度解析:高性能Web服务器与实时应用构建
- 掌握深度图技术:游戏开发中的绚丽应用案例
- Dart语言的HTTP扩展包功能详解
- MoonMaker: 投资组合加固神器,助力$GME投资者登月
- 计算机毕业设计答辩PPT模板下载