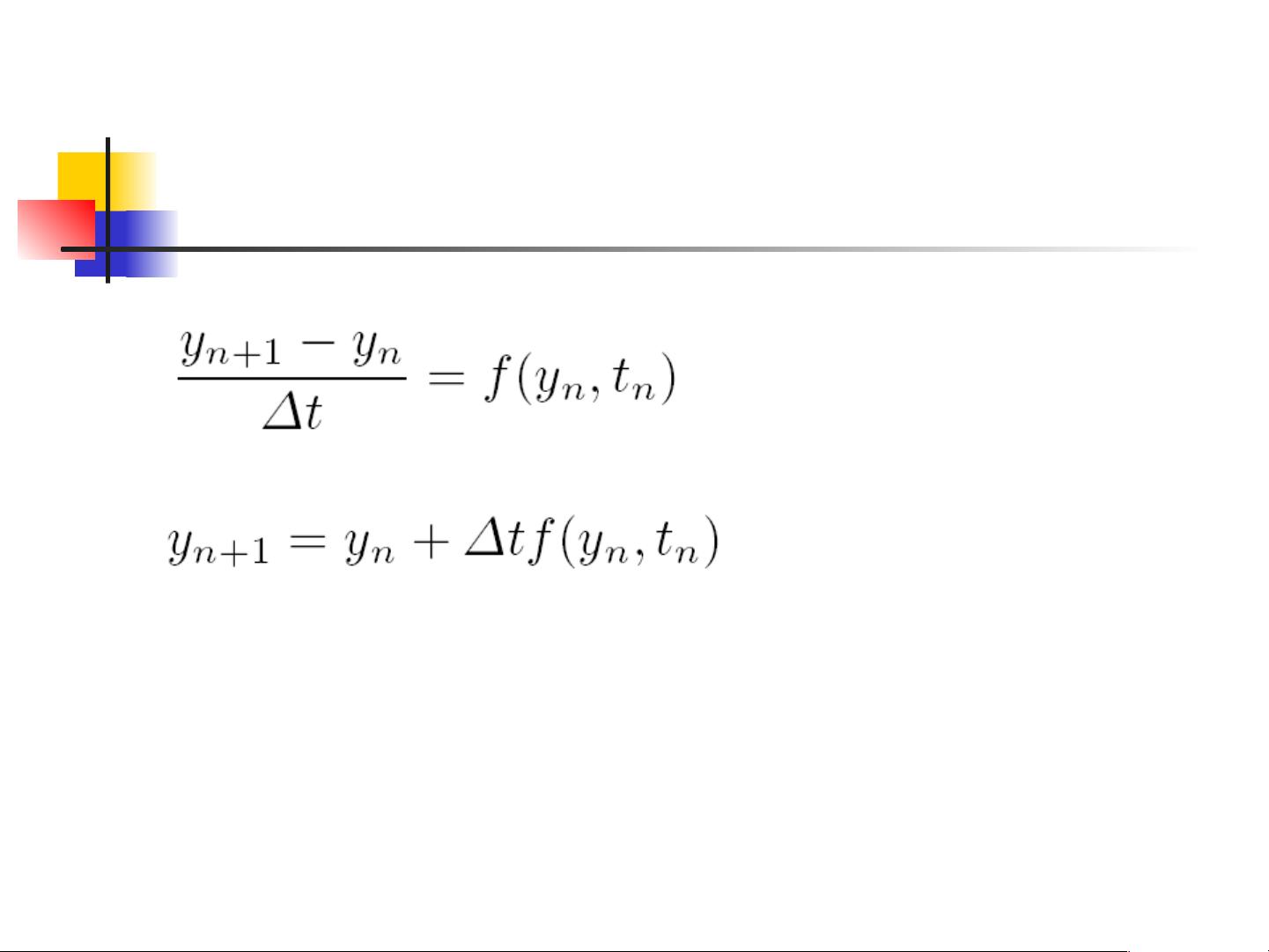MATLAB数值分析基础教程：第7章-数值微分与Euler方法

本资源是《Matlab应用基础教程》系列课程的第七章，专门讲解基于Matlab的数值分析方法。该章深入探讨了数值微分这一关键概念，它是数学建模和工程问题求解中的重要工具。章节开始时，通过离散化连续函数和选取足够小的步长h来解释数值微分的原理，强调了h的选择应能满足误差控制的要求，这里提到的Matlab中的最小数eps就是一个常用的标准。 数值微分部分，以计算sin(pi/3)的导数为例，展示了如何利用Matlab中的简单算术运算来实现近似微分。此外，还介绍了Euler's method（欧拉法），这是一种用于求解微分方程数值解的常用数值积分方法，它通过递推迭代算法在循环结构中进行计算。 接下来，以一个实际问题为例，教授如何用Matlab编写程序，通过while循环和递推迭代来求解初始条件下的微分方程，直到达到特定时间点。这种方法的优点在于其简洁和空间效率，但缺点是无法保存每个时间步的中间状态。 课程进一步鼓励学生通过比较分析解和数值解的图形表示，来验证和理解数值微分方法的有效性和精度。通过Matlab的plot函数，学生可以看到数值解与精确解的对比，这对于理解和评估数值方法的性能至关重要。 本章内容涵盖了数值微分的基础理论、Matlab编程实现以及实际问题的解决策略，是深入理解Matlab在数值分析中的应用的重要环节，适合对Matlab有基本了解的学习者进行进阶学习或复习。对于想要掌握数值计算技巧的工程师和科研人员来说，这是提升技能的一个宝贵资源。全套课程提供了全面且循序渐进的学习路径，有助于系统性地掌握Matlab在工程和科研领域的实用技巧。